Posts
-
RE: Import multiple Takes
Hey @yannickkohn,
Thank you for the source code, but pseudo code is often problematic, especially when it contains so many undefined functions. I cannot say much about any bugs, as your code is so 'pseudo' and you do not show the really deep down work (reading curves and keys here).
What also is a bit weird is that you use
FindOverride. That function is private for a reason. You should set the active take and then just evaluate the scene data or the tracks of scene data when you are interested in animations only.Cheers,
Ferdinand -
RE: Import multiple Takes
Hey Yannick, as I said without code and your scene data we will not be able to help you. In understand what you want to do conceptually, but for concrete help we will need concrete code and concrete data. As I hinted at, not all aspects of takes can be faithfully exported into the Melange (a.k.a.) Cineware format. The Take export has be initially written for the Adobe After Effects bindings, so there might be gaps even when data could be discretized in principle.
-
RE: Import multiple Takes
Hello @yannickkohn,
Welcome to the Maxon developers forum and its community, it is great to have you with us!
Getting Started
Before creating your next postings, we would recommend making yourself accustomed with our forum and support procedures. You did not do anything wrong, we point all new users to these rules.
- Forum Overview: Provides a broad overview of the fundamental structure and rules of this forum, such as the purpose of the different sub-forums or the fact that we will ban users who engage in hate speech or harassment.
- Support Procedures: Provides a more in detail overview of how we provide technical support for APIs here. This topic will tell you how to ask good questions and limits of our technical support.
- Forum Features: Provides an overview of the technical features of this forum, such as Markdown markup or file uploads.
It is strongly recommended to read the first two topics carefully, especially the section Support Procedures: How to Ask Questions.
About your First Question
It is quite hard to answer your question in this form, please read the points listed above. From what I get, you have some C++ application and use there the Cineware SDK to import c4d files. You now want to read take data in these scenes. First of all, I would recommend to read the end user docs on takes, in case you have not already.
Takes are somewhat comparable to render settings in Cinema 4D, as in that you always have at least one of them in a scene, but also can have many (which also can be nested). Just likes for render settings, there can only be one active take at a time. So unless you have called SetCurrentTake, the data of your scene will not change.
Cineware is also a sparse/discrete data format, i.e., all procedural goodness of Cinema 4D has been baked down. Without knowing what take data you want to see being exported, it is hard to tell if what you are experiencing is working as intended or not. Please share your code and images or files of the scene you are trying to export, including examples/descriptions of what data is missing.
Cheers,
Ferdinand -
RE: how to detect obj selected in InExcludeData()?
Hey @chuanzhen,
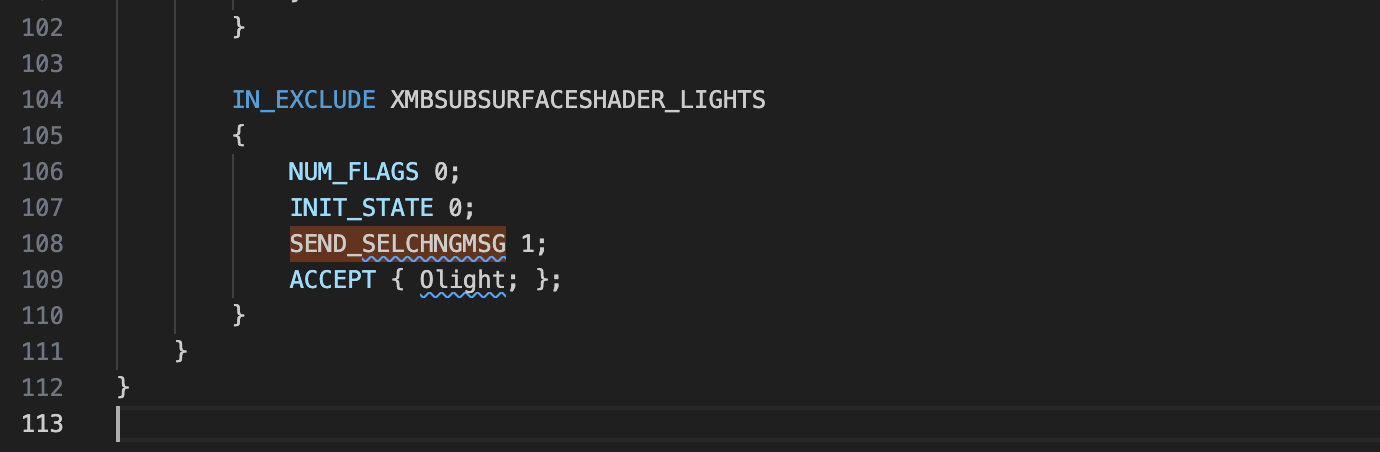
Thank you for reaching out to us. For me this works fine, but I also struggled for a second with this. The crucial information is probably that you have to set
SEND_SELCHNGMSGin theInExcludeCustomGuifor which this shall work. Since this information is rather obscure, I have updated the docs ofInExcludeData::GetDatato better reflect this.Cheers,
Ferdinand -
RE: [Cinema 4D/Redshift] Nested Redshift Proxy Files Not Detected by Project Asset Inspector
Hello @vaishhg,
Welcome to the Maxon developers forum and its community, it is great to have you with us!
Getting Started
Before creating your next postings, we would recommend making yourself accustomed with our forum and support procedures. You did not do anything wrong, we point all new users to these rules.
- Forum Overview: Provides a broad overview of the fundamental structure and rules of this forum, such as the purpose of the different sub-forums or the fact that we will ban users who engage in hate speech or harassment.
- Support Procedures: Provides a more in detail overview of how we provide technical support for APIs here. This topic will tell you how to ask good questions and limits of our technical support.
- Forum Features: Provides an overview of the technical features of this forum, such as Markdown markup or file uploads.
It is strongly recommended to read the first two topics carefully, especially the section Support Procedures: How to Ask Questions.
About your First Question
I assume this is about Deadline? I am also not sure that I understand the question correctly. Let me recap, so that we are sure we talk about the same thing.
You have a scene
Original.c4dand you export it to the Redshift Scene formatOriginalProxy.rs. Then you create a Cinema 4D sceneComposition.c4dand there create one or multiple Redshift Proxy objects referencingOriginalProxy.rs. Then you export that scene as a Redshift scene asCompositionProxy.rs. You now want to access information aboutOriginal.c4dorOriginalProxy.rswhen loadingCompositionProxy.rswith a RS Proxy object into a Cinema 4D scene (or by extension see that information in the Asset Inspector).That is not possible.
rsis the Redshift scene format which works across the full landscape of DCCs supported by Redshift. The Redshift format has no such concept as a generator and just discretizes all smooth/procedural geometry data.When you export a Cinema 4D scene to the Redshift
rsformat, it will among other things just walk your scene and collect all the geometry caches and save them discretely in the RS format. For Redshift it does not make any difference if it collects the cache of a Cube generator object or the cache of a Redshift Proxy generator object. In the eyes of Redshift these are both just two procedural geometry generators which must be discretized/baked for export (not entirely true, because Redshift Proxy objects are cached in the Redshift Core itself and not in Cinema 4D, but close enough).As soon as you save a scene in the
RSformat, all information is lost that something once was a generator and the parameters it held. The Redshift Core also does not know a concept such as asset data or the Asset Inspector, as that is a Cinema 4D specific concept. So, such data is not stored in thersformat either.So, to answer your questions: You cannot reach into the past like that. Neither directly via the Asset Inspector and its API, nor indirectly by for example traversing the scene graph of a scene. In fact, RS Proxy objects do not even have caches in the Cinema 4D world, unless you set Preview to Mesh. The actual data resides discretely in the in the Redshift Core.
As an example, when we have this scene which holds two proxies and we run this script on it to, print the scene graph string of each object in the scene, we can see both proxies only hold discrete polygonal data:
import c4d import mxutils doc: c4d.documents.BaseDocument # The currently active document. def main() -> None: """Called by Cinema 4D when the script is being executed. """ for obj in mxutils.IterateTree(doc.GetFirstObject(), True): print(mxutils.GetSceneGraphString(obj)) if __name__ == '__main__': main()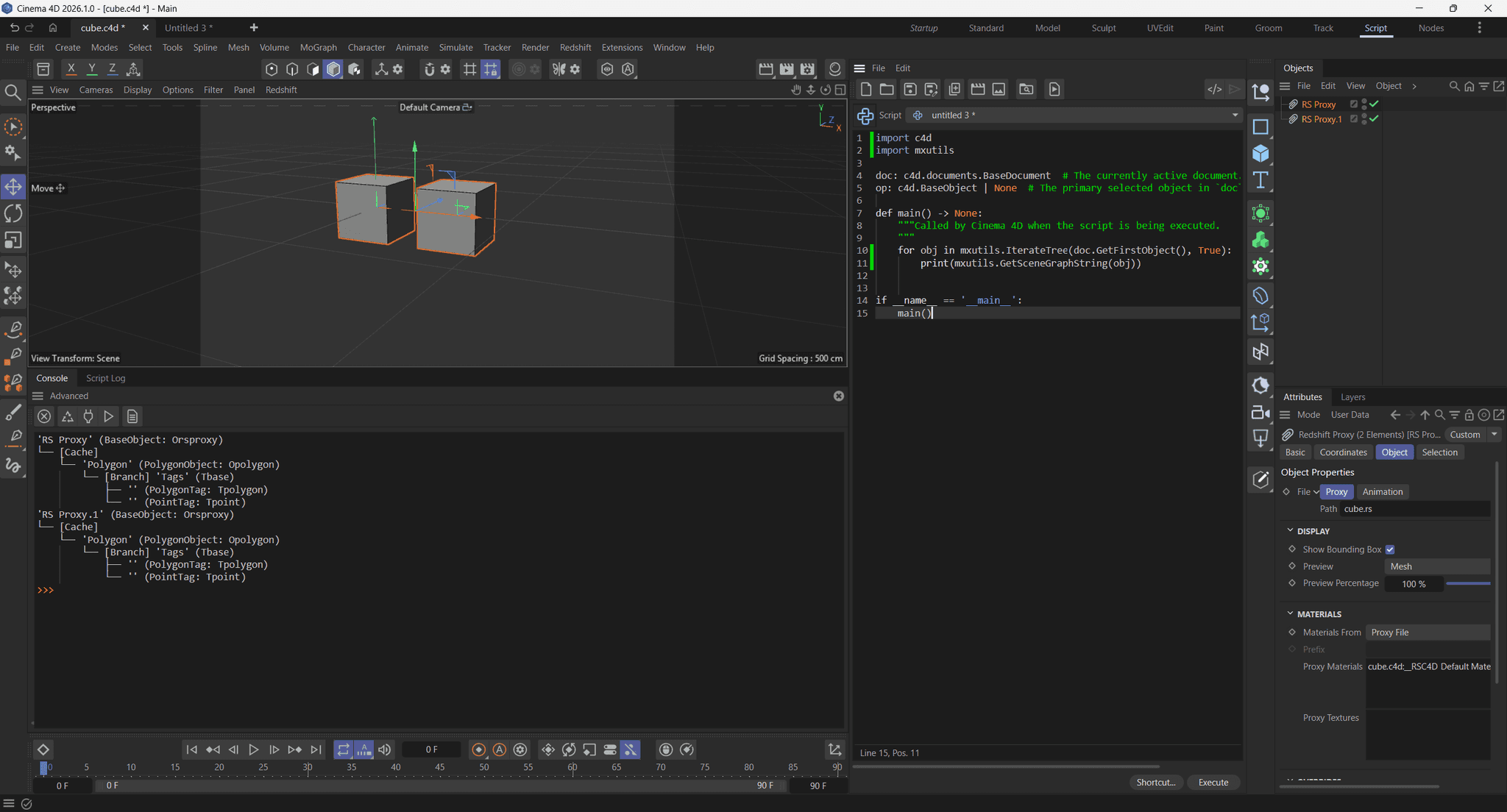
When we now save that scene as an RS scene file and load that in an RS Proxy object in another scene, we will see that it only contains one blob of discrete geometry.
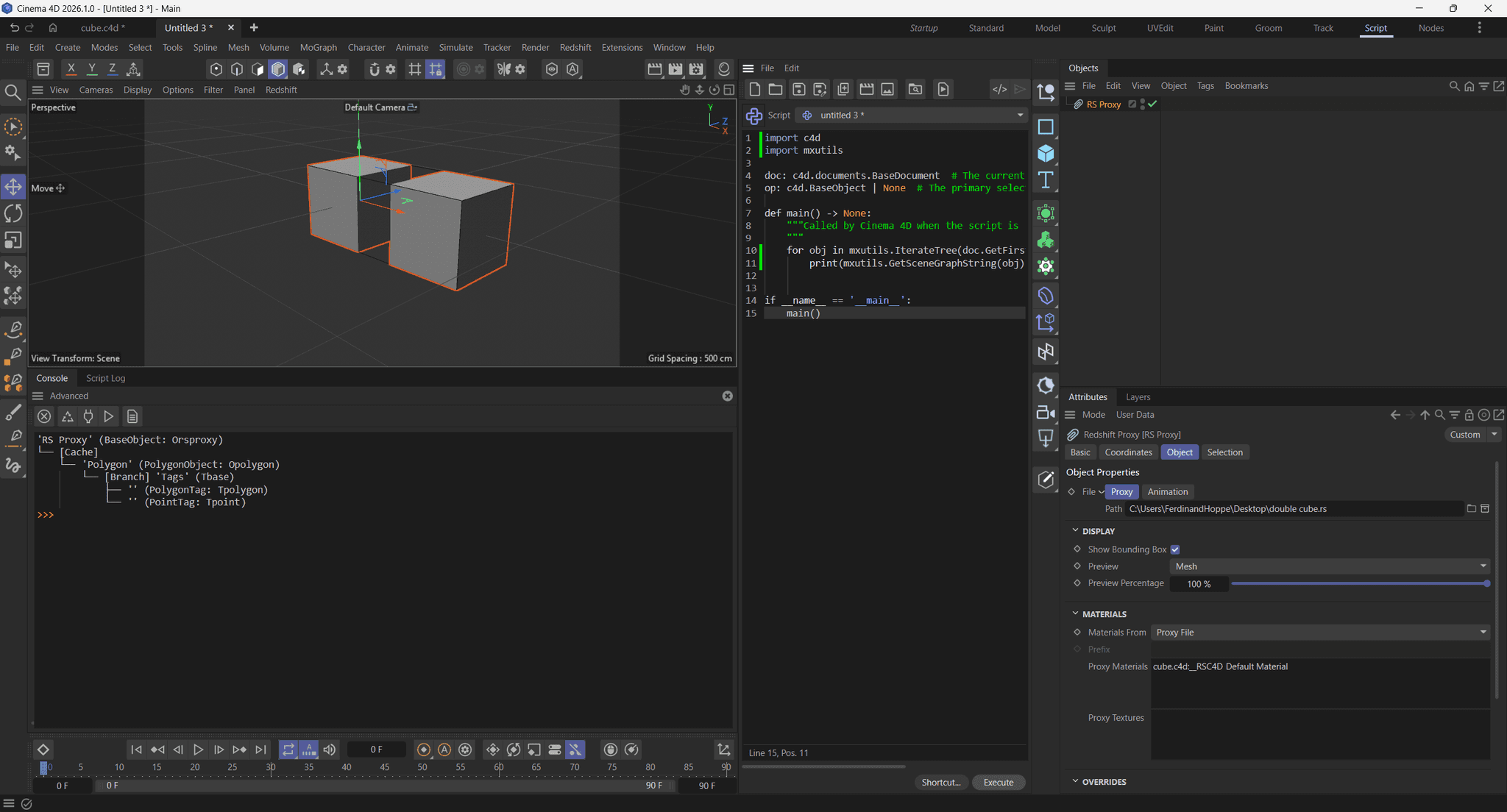
Cheers,
Ferdinand -
RE: Finding out the latest asset version number/string via python
Hey @MPB,
there is no need to be sorry, sometimes one struggles even with very on the nose information. But the example is quite verbose, as it contains literally the words "version" and "timestamp" multiple times and explains how these concepts work.
But it is pointless to endlessly discuss this, it is quicker for me to just write what you want. Here is an example doing exactly what you want to do. Please understand that it is an exception that I write a code example when there is already an example which already explains the subject sufficiently as it is here the case.
Cheers,
FerdinandResult
What we also learn from this, is that the asset team works at unholy hours
 .
.Latest version of asset file_266f97c45ea05f17 has version string '2.0.2 - 2022-07-30 02:29', version hash '4905fdf9a02aa951e0d18a6d07f244172a41205a4692b4ae065d6b856e5de7cb' and timestamp '2022-07-30 00:29:28'. Found 4 asset versions for asset id file_266f97c45ea05f17: Found asset version with version string '2.0.2 - 2022-07-30 02:29', version hash '4905fdf9a02aa951e0d18a6d07f244172a41205a4692b4ae065d6b856e5de7cb' and timestamp '2022-07-30 00:29:28'. Found asset version with version string '2.0.1 - 2022-02-03 23:45', version hash '3997955fa22c74286c9319509eeaa7a5dccd0230951b608fe338741bbce0d9f9' and timestamp '2022-02-03 22:45:45'. Found asset version with version string '2.0.0 - 2022-02-03 23:26', version hash '310c1a6684d8be9eafff1708225b64fe72bff46bd7fae8fa783c39fac7c70d43' and timestamp '2022-02-03 22:26:39'. Found asset version with version string '1.0.1 - 2022-02-02 03:02', version hash '5fafa425cbd3f951d4ce8859fc02f51857342094dd0c2fcac8eb4377b7cea9dd' and timestamp '2022-02-02 02:02:47'. Assets sorted by timestamp: file_266f97c45ea05f17/5fafa425cbd3f951d4ce8859fc02f51857342094dd0c2fcac8eb4377b7cea9dd (1.0.1 - 2022-02-02 03:02) file_266f97c45ea05f17/310c1a6684d8be9eafff1708225b64fe72bff46bd7fae8fa783c39fac7c70d43 (2.0.0 - 2022-02-03 23:26) file_266f97c45ea05f17/3997955fa22c74286c9319509eeaa7a5dccd0230951b608fe338741bbce0d9f9 (2.0.1 - 2022-02-03 23:45) file_266f97c45ea05f17/4905fdf9a02aa951e0d18a6d07f244172a41205a4692b4ae065d6b856e5de7cb (2.0.2 - 2022-07-30 02:29)Code
#coding: utf-8 """Provides an example for sorting assets by their time stamp metadata. """ __version__ = "2026.X.X" import c4d import maxon def main() -> None: """Runs the example for reading asset metadata. """ # Get the user preferences repository. repo: maxon.AssetRepositoryRef = maxon.AssetInterface.GetUserPrefsRepository() if not repo: raise RuntimeError("Could not access the user preferences repository.") # The id of the "Stone 01" asset which naturally has four asset versions. aid: maxon.Id = maxon.Id("file_266f97c45ea05f17") # Find explicitly the latest version of the asset. asset: maxon.AssetDescription = repo.FindLatestAsset( maxon.AssetTypes.File(), aid, maxon.Id(), maxon.ASSET_FIND_MODE.LATEST) # Get the time stamp and version hash and string of the latest asset version. metadata: maxon.AssetMetaData = asset.GetMetaData() timestamp: str = metadata.Get(maxon.ASSETMETADATA.ASSET_TIMESTAMP) version_hash: str = asset.GetVersion() version_string: str = maxon.AssetInterface.GetVersionString(asset) print(f"Latest version of asset {aid} has version string '{version_string}', " f"version hash '{version_hash}' and timestamp '{timestamp}'.") # Now find all versions of assets with the id #aid and print their metadata. assets: list[maxon.AssetDescription] = repo.FindAssets( maxon.AssetTypes.File(), aid, maxon.Id(), maxon.ASSET_FIND_MODE.ALL) print(f"\nFound {len(assets)} asset versions for asset id {aid}:") for item in assets: metadata = item.GetMetaData() timestamp = metadata.Get(maxon.ASSETMETADATA.ASSET_TIMESTAMP) version_hash = item.GetVersion() version_string = maxon.AssetInterface.GetVersionString(item) print(f"Found asset version with version string '{version_string}', " f"version hash '{version_hash}' and timestamp '{timestamp}'.") # So, if we wanted to temporally sort #assets, we could do this. The asset version is naturally # a hash, and there is no grantee that there is a version string or that that string is parsable # into a numeric value which could be sorted. assets.sort(key=lambda a: a.GetMetaData().Get(maxon.ASSETMETADATA.ASSET_TIMESTAMP)) print("\nAssets sorted by timestamp:") for item in assets: print(f"{item} ({maxon.AssetInterface.GetVersionString(item)})") if __name__ == "__main__": main() -
RE: Object-level "Show Help" (CMD+F1) for ObjectData plugins?
Hey @lasselauch,
Thank you for reaching out to us. I am not 100% sure that I am understanding you correctly. You basically want to hook into this menu entry, right?

That is not possible at the moment. Because what this thing does, is gather information from the description of the selected entity or the active dialog and with that data calls cinema::OpenHelpBrowser (at least the backend version of that function). This is not even a dedicated command, just a switch case within the abstracted dialog menu handling. So, this is custom built for
help.maxon.net.It would not be impossible to isolate this so that there could be either a dedicated plugin hook for this or it somehow reusing the existing
RegisterPluginHelpDelegate(the C++ variant of the Python hook you used). But that would be quite a bit of work, and you would also have to answer if that justifies the overhead of calling all hooks each time a user presses that button/menu entry (but you could also argue that the overhead ofRegisterPluginHelpDelegateis even worse).I can see the allure of "Show Help" working for third parties, but I doubt many people would use it and the current system is very Maxon centric which are not good arguments for going for this. On top of this, in theory, it would have to support both
NodeDataentities and dialogs (because the menu entry works for both). We could only support nodes, but there I would just recommend the proven and tested workflow of including a base description at the end of your nodes, which places there a bitmap icon branding that is clickable or just a button. I talked a bit in the all new Licensing Manual videos and code about this workflow.edit: An alternative could be to offer a hook into
OpenHelpBrowserbut there you probably then run into problems with dialogs as the back end function splits into two signatures (which do not exist in the frontend). Also solvable but again extra work that can hardly be justified but the few users this will have.I am not strictly against adding such hook, but I currently do not see a good cost/effect ratio unless this thread is flooded with third party developers stating otherwise.
Cheers,
Ferdinand -
RE: Finding out the latest asset version number/string via python
Hey,
as I already explained,
maxon.ASSET_FIND_MODE.LATESTensures that you find the last version of an asset. So this line of yours:asset_desc = repo.FindLatestAsset(maxon.AssetTypes.File().GetId(), temp_id, maxon.Id(), maxon.ASSET_FIND_MODE.LATEST)will retrieve the last asset version of an asset with the ID
temp_idwhich is of asset typeFile. If you would usemaxon.ASSET_FIND_MODE.ALLfor example and then also notFindLatestAssetbutFindAssets, you would find all assets that have the IDtemp_id.The id of an asset is not necessarily unique within a repository. It shares its ID with all other versions of that asset. Only the ID and version can uniquely identify an asset. And as said before, the version of an asset does not have to be a (quasi) numeric value as you assume it to be. The asset version is always a string, and in some cases, for example in the code example I linked to above, people put there something that could be parsed into a numeric value. But the asset version can also just be the string 'Bob's your uncle' or just some hash. So, you cannot sort assets temporally by their asset version. It is just another identifier that makes that version unique within the namespace of the asset ID.
If you want to temporally sort asset versions, first search for all assets with that ID, and then sort them using their timestamp. This, asset versioning, time stamps and other asset metadata, all has been extensively covered in the code example I already linked to above. Please read the example.
Cheers,
Ferdinand -
RE: Finding out the latest asset version number/string via python
Hello @MPB,
Welcome to the Maxon developers forum and its community, it is great to have you with us!
Getting Started
Before creating your next postings, we would recommend making yourself accustomed with our forum and support procedures. You did not do anything wrong, we point all new users to these rules.
- Forum Overview: Provides a broad overview of the fundamental structure and rules of this forum, such as the purpose of the different sub-forums or the fact that we will ban users who engage in hate speech or harassment.
- Support Procedures: Provides a more in detail overview of how we provide technical support for APIs here. This topic will tell you how to ask good questions and limits of our technical support.
- Forum Features: Provides an overview of the technical features of this forum, such as Markdown markup or file uploads.
It is strongly recommended to read the first two topics carefully, especially the section Support Procedures: How to Ask Questions.
About your First Question
Without your code and the asset you are trying to read, helping youn concretely is impossible. Asset versioning is demonstrated pretty throughly in this code example.
I think your major misconception is that an asset version string has to be what you would consider a version descriptor, .e.g., "1.0". But that is absolutely not the case, and you can put there anything you want. The system will by default put there hashes; which is probably what you mean with "some kind of ID".
You must evaluate the date of last modification of each version of an asset to temporally order them. But that is all not really necessary when you just want to get the last version of an asset, as that is already baked into search operations with
maxon.ASSET_FIND_MODE.LATEST. I.e., when you have either an asset ID or an asset description, you just search for that asset ID and set the find mode to latest. See this example for a concrete case.You can also search for all versions of an asset and then sort them yourself via the time stamp (see also first example link). You can also access the other versions of an asset if you have just one asset description, as each asset links to its other versions with a list of asset-id-version tuples.
Cheers,
Ferdinand -
RE: How to access animation tracks for a GraphNode in a capsule
Hello @kng_ito,
thank you for reaching out to us. The answer to your question is
BaseList2Dand NimbusBaseInterface, as they both in tandem realize the relationship between Cinema and Maxon API scene elements. What node materials offer is just a convenience interface which is also offered in a more generic way via the mentioned classes.A
BaseList2Dis the base type for a generic Cinema API scene element that holds a data container. It also offers methods to retrieve one or manyNimbusBaseInterfacereferences for that element, each associating this element of a Cinema API scene with a Maxon API nodes graph. A node material will for example have oneNimbusBaseInterfacereference for each material node space (i.e., render engine and with that node graph) it supports.I actually thought there were already forum posts or even a code example about this subject, but I could not find any. So, I created a small code example addressing exactly this topic, as this is probably something people want to do commonly. It will be part of an upcoming Python SDK, but you can find a draft version below. The code is not that complicated, but the subject/theory around it is not entirely trivial. So, it is one of these code examples which is more words than code. I hope this helps you to understand the relationship between Cinema API scene elements and Maxon API nodes graphs better.
Cheers,
FerdinandResult
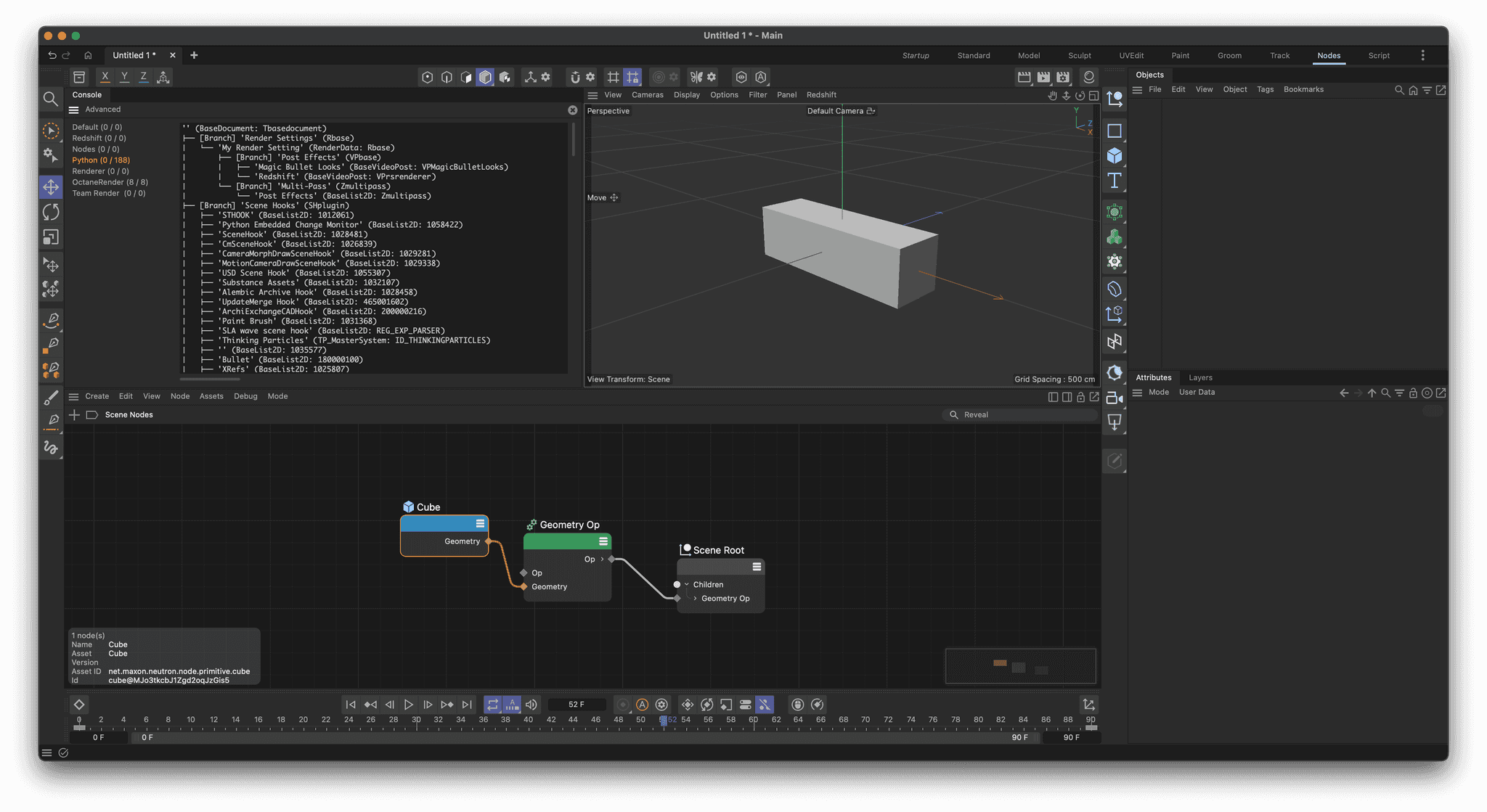
'' (BaseDocument: Tbasedocument) ├── [Branch] 'Render Settings' (Rbase) │ └── 'My Render Setting' (RenderData: Rbase) │ ├── [Branch] 'Post Effects' (VPbase) │ │ ├── 'Magic Bullet Looks' (BaseVideoPost: VPMagicBulletLooks) │ │ └── 'Redshift' (BaseVideoPost: VPrsrenderer) │ └── [Branch] 'Multi-Pass' (Zmultipass) │ └── 'Post Effects' (BaseList2D: Zmultipass) ├── [Branch] 'Scene Hooks' (SHplugin) │ ├── 'STHOOK' (BaseList2D: 1012061) │ ├── 'Python Embedded Change Monitor' (BaseList2D: 1058422) │ ├── 'SceneHook' (BaseList2D: 1028481) │ ├── 'CmSceneHook' (BaseList2D: 1026839) │ ├── 'CameraMorphDrawSceneHook' (BaseList2D: 1029281) │ ├── 'MotionCameraDrawSceneHook' (BaseList2D: 1029338) │ ├── 'USD Scene Hook' (BaseList2D: 1055307) │ ├── 'Substance Assets' (BaseList2D: 1032107) │ ├── 'Alembic Archive Hook' (BaseList2D: 1028458) │ ├── 'UpdateMerge Hook' (BaseList2D: 465001602) │ ├── 'ArchiExchangeCADHook' (BaseList2D: 200000216) │ ├── 'Paint Brush' (BaseList2D: 1031368) │ ├── 'SLA wave scene hook' (BaseList2D: REG_EXP_PARSER) │ ├── 'Thinking Particles' (TP_MasterSystem: ID_THINKINGPARTICLES) │ ├── '' (BaseList2D: 1035577) │ ├── 'Bullet' (BaseList2D: 180000100) │ ├── 'XRefs' (BaseList2D: 1025807) │ ├── 'CAManagerHook' (BaseList2D: 1019636) │ │ └── [Branch] 'Weights Handler Head' (Tbaselist2d) │ │ └── 'Weights Handler' (BaseList2D: 1037891) │ ├── 'Volume Save Manager Hook' (BaseList2D: 1040459) │ ├── 'UV Display 3D SceneHook' (BaseList2D: 1054166) │ ├── 'uvhook' (BaseList2D: 1053309) │ ├── 'ScatterPlacementHook' (BaseList2D: 1058060) │ ├── 'Tool System Hook' (BaseList2D: ID_TOOL_SYSTEM_HOOK) │ │ └── [Branch] 'SBM' (431000215) │ │ └── 'Symmetry node' (BaseList2D: 431000215) │ │ └── [Branch] 'C4DCoreWrapper' (200001044) │ │ └── 'Symmetry node - net.maxon.symmetry.context.modeling' (BaseList2D: 300001078) │ ├── 'MoGraphSceneHook' (BaseList2D: 1019525) │ ├── 'gozScenehook' (BaseList2D: 1059748) │ ├── 'Octane X' (BaseList2D: 1030798) │ ├── 'Simulation' (BaseList2D: ID_SIMULATIONSCENE_HOOK) │ │ └── [Branch] 'Simulation World' (Obase) │ │ └── 'Default Simulation Scene' (BaseObject: Osimulationscene) │ ├── 'PersistentHook' (BaseList2D: 180420202) │ ├── 'Scene Nodes' (BaseList2D: SCENENODES_IDS_SCENEHOOK_ID) │ │ └── [Branch] 'Nodes' (300001078) │ │ ├── 'Group' (BaseList2D: 300001078) │ │ ├── 'Group' (BaseList2D: 300001078) │ │ ├── 'Group' (BaseList2D: 300001078) │ │ ├── 'Geometry Op' (BaseList2D: 300001078) │ │ ├── 'Scene Root' (BaseList2D: 300001078) │ │ └── 'Cube' (BaseList2D: 300001078) │ │ └── [Branch] 'Tracks' (CTbase) │ │ ├── 'Size . X' (CTrack: CTbase) │ │ │ └── [Branch] 'Sequences' (CSbase) │ │ │ └── '' (CCurve: CSbase) │ │ ├── 'Size . Y' (CTrack: CTbase) │ │ │ └── [Branch] 'Sequences' (CSbase) │ │ │ └── '' (CCurve: CSbase) │ │ └── 'Size . Z' (CTrack: CTbase) │ │ └── [Branch] 'Sequences' (CSbase) │ │ └── '' (CCurve: CSbase) │ ├── 'NE_SceneHook' (BaseList2D: 465002367) │ ├── 'Take Hook' (BaseList2D: 431000055) │ │ └── [Branch] 'Take System Branch' (TakeBase) │ │ └── 'Main' (BaseTake: TakeBase) │ │ └── [Branch] 'Override Folders' (431000073) │ │ └── 'Overrides' (BaseList2D: 431000073) │ │ ├── 'Others' (BaseList2D: 431000073) │ │ ├── 'Layers' (BaseList2D: 431000073) │ │ ├── 'Materials' (BaseList2D: 431000073) │ │ ├── 'Shaders' (BaseList2D: 431000073) │ │ ├── 'Tags' (BaseList2D: 431000073) │ │ └── 'Objects' (BaseList2D: 431000073) │ ├── 'CombineAc18_AutoCombine_SceneHook' (BaseList2D: 1032178) │ ├── 'PLKHUD' (BaseList2D: 1020132) │ │ └── [Branch] 'PSUNDOHEAD' (Obase) │ │ └── 'PKHOP' (BaseObject: 1020120) │ ├── 'RenderManager Hook' (BaseList2D: 465003509) │ ├── 'Sound Scrubbing Hook' (BaseList2D: 100004815) │ ├── 'To Do' (BaseList2D: 465001536) │ ├── 'Animation' (BaseList2D: 465001535) │ ├── 'BaseSettings Hook' (BaseList2D: ID_BS_HOOK) │ ├── '' (BaseList2D: 1060457) │ ├── 'SculptBrushModifierSceneHook' (BaseList2D: 1030499) │ ├── 'Sculpt Objects' (BaseList2D: 1024182) │ ├── 'HairHighlightHook' (BaseList2D: 1018870) │ ├── 'MeshObject Scene Hook' (BaseList2D: 1037041) │ ├── 'Lod Hook' (BaseList2D: 431000182) │ ├── 'Annotation Tag SceneHook' (BaseList2D: 1030679) │ ├── 'Sniper' (BaseList2D: 430000000) │ ├── 'Mesh Check Hook' (BaseList2D: 431000027) │ ├── 'Modeling Objects Hook' (BaseList2D: 431000032) │ │ └── [Branch] 'Modeling Objects Branch' (431000031) │ │ ├── 'Pattern Direction Manipulator' (BaseObject: Opatternmanipulator) │ │ ├── 'Plane Manipulator' (BaseObject: Oplanemanipulator) │ │ ├── 'Pivot Manipulator' (BaseObject: Opivotmanipulator) │ │ ├── 'Knife Line Manipulator' (BaseObject: 431000168) │ │ ├── 'Subdivision Manipulator' (BaseObject: 431000172) │ │ └── 'PolyPenObject' (BaseObject: 431000031) │ ├── 'Snap Scenehook' (BaseList2D: 440000111) │ │ ├── [Branch] 'WpSH' (440000111) │ │ │ └── 'WorkPlane' (BaseObject: Oworkplane) │ │ └── [Branch] 'MdSH' (Tbase) │ │ └── 'Modeling Settings' (BaseList2D: 440000140) │ ├── 'Doodle Hook' (BaseList2D: 1022212) │ ├── 'Stereoscopic' (BaseList2D: 450000226) │ ├── 'ViewportExtHookHUD' (BaseList2D: ID_VIEW_SCENEHOOKHUD) │ ├── 'ViewportExtHookhighlight' (BaseList2D: ID_VIEW_SCENEHOOKHIGHLIGHT) │ ├── 'MeasureSceneHook' (BaseList2D: ID_MEASURE_SCENEHOOK) │ ├── 'Redshift' (BaseList2D: 1036748) │ ├── 'GvHook' (BaseList2D: ID_SCENEHOOK_PLUGIN) │ ├── 'Material Scene Hook' (BaseList2D: 300001077) │ ├── 'TargetDistancePicker' (BaseList2D: 1028063) │ └── 'BodyPaint SceneHook' (BaseList2D: 1036428) └── [Branch] '' (Tbasedraw) └── '' (BaseList2D: 110306) --- Maxon API Scene Nodes Data --- Maxon API node: net.maxon.neutron.scene.root -> Cinema API surrogate node: <c4d.BaseList2D object called Scene Root with ID 300001078 at 22186209472> Input port: net.maxon.neutron.scene.root/_0<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/_0<in/flags -> DescID: ((1768828774, 5, 0), (1818322803, 12, 0)) Input port: net.maxon.neutron.scene.root/_0<filter -> DescID: ((1718185076, 5, 0), (1701969920, 5, 0), (1, 400006001, 0)) Input port: net.maxon.neutron.scene.root/_0/rot<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/_0/rot<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<in2 -> DescID: ((1768829440, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<in1 -> DescID: ((1768829184, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root<net.maxon.neutron.op.objectbase.children -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848536677, 5, 0), (1970565743, 5, 0), (1848536944, 5, 0), (779051626, 5, 0), (1701016674, 5, 0), (1634952494, 5, 0), (1667787116, 5, 0), (1685218670, 5, 0), (593719149, 5, 0), (1835101796, 5, 0), (593585252, 5, 0), (1986097769, 5, 0), (1633970531, 5, 0), (1886351988, 8, 0)) Input port: net.maxon.neutron.scene.root<net.maxon.neutron.op.objectbase.children/_0 -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848536677, 5, 0), (1970565743, 5, 0), (1848536944, 5, 0), (779051626, 5, 0), (1701016674, 5, 0), (1634952494, 5, 0), (1667787116, 5, 0), (1685218670, 5, 0), (774975086, 5, 0), (1702112877, 5, 0), (1635282798, 5, 0), (778986869, 5, 0), (1953656686, 5, 0), (779055150, 5, 0), (1868720741, 5, 0), (1668571745, 5, 0), (1936010851, 5, 0), (1751739492, 5, 0), (1919249920, 5, 0), (1, 133, 0)) Maxon API node: net.maxon.neutron.scene.root/_0 -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 22186202432> Input port: net.maxon.neutron.scene.root/_0<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/_0<in/flags -> DescID: ((1768828774, 5, 0), (1818322803, 12, 0)) Input port: net.maxon.neutron.scene.root/_0<filter -> DescID: ((1718185076, 5, 0), (1701969920, 5, 0), (1, 400006001, 0)) Input port: net.maxon.neutron.scene.root/_0/rot<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/_0/rot<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Maxon API node: net.maxon.neutron.scene.root/_0/rot -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 22186170048> Input port: net.maxon.neutron.scene.root/_0/rot<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/_0/rot<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Maxon API node: net.maxon.neutron.scene.root/concat -> Cinema API surrogate node: None Maxon API node: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0 -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 22186170048> Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<in2 -> DescID: ((1768829440, 5, 0), (1, 133, 0)) Input port: net.maxon.neutron.scene.root/net.maxon.neutron.corenode.multransform_0<in1 -> DescID: ((1768829184, 5, 0), (1, 133, 0)) Maxon API node: geometry@WCuZ0OX$L9brZcIW8Vdmn6 -> Cinema API surrogate node: <c4d.BaseList2D object called Geometry Op with ID 300001078 at 22186209472> Input port: geometry@WCuZ0OX$L9brZcIW8Vdmn6<geometry -> DescID: ((1734700909, 5, 0), (1702130297, 5, 0), (1, 133, 0)) Input port: geometry@WCuZ0OX$L9brZcIW8Vdmn6<net.maxon.node.bypassable.bypass -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848536687, 5, 0), (1684352610, 5, 0), (2037408115, 5, 0), (1935762028, 5, 0), (1697538681, 5, 0), (1885434739, 5, 0), (1, 400006001, 0)) Maxon API node: cube@MJo3tkcbJ1Zgd2oqJzGis5 -> Cinema API surrogate node: <c4d.BaseList2D object called Cube with ID 300001078 at 22186170048> Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.cube.subz -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778270050, 5, 0), (1697543029, 5, 0), (1652162560, 5, 0), (1, 15, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.cube.suby -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778270050, 5, 0), (1697543029, 5, 0), (1652097024, 5, 0), (1, 15, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.cube.subx -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778270050, 5, 0), (1697543029, 5, 0), (1652031488, 5, 0), (1, 15, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.fillets.segment -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778463596, 5, 0), (1818588275, 5, 0), (779314535, 5, 0), (1835363956, 5, 0), (1, 15, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.fillets.radius -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778463596, 5, 0), (1818588275, 5, 0), (779247972, 5, 0), (1769304832, 5, 0), (1, 19, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.fillets.enable -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778463596, 5, 0), (1818588275, 5, 0), (778399329, 5, 0), (1651270912, 5, 0), (1, 400006001, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.cube.separate -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (778270050, 5, 0), (1697543013, 5, 0), (1885434465, 5, 0), (1952776192, 5, 0), (1, 400006001, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.size -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (779315578, 5, 0), (1694498816, 5, 0), (1, 23, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.size/*access*zin -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (779315578, 5, 0), (1697589857, 5, 0), (1667458419, 5, 0), (1932163689, 5, 0), (1845493760, 5, 0), (1, 19, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.size/*access*xin -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (779315578, 5, 0), (1697589857, 5, 0), (1667458419, 5, 0), (1932163177, 5, 0), (1845493760, 5, 0), (1, 19, 0)) Input port: cube@MJo3tkcbJ1Zgd2oqJzGis5<net.maxon.command.modeling.primitive.size/*access*yin -> DescID: ((1852142638, 5, 0), (1835104367, 5, 0), (1848533871, 5, 0), (1835884910, 5, 0), (1680764271, 5, 0), (1684368489, 5, 0), (1852255856, 5, 0), (1919511913, 5, 0), (1953068645, 5, 0), (779315578, 5, 0), (1697589857, 5, 0), (1667458419, 5, 0), (1932163433, 5, 0), (1845493760, 5, 0), (1, 19, 0)) Maxon API node: cube@MJo3tkcbJ1Zgd2oqJzGis5/parambuilder -> Cinema API surrogate node: None Maxon API node: cube@MJo3tkcbJ1Zgd2oqJzGis5/defaultselections -> Cinema API surrogate node: None Maxon API node: cube@MJo3tkcbJ1Zgd2oqJzGis5/generategeometry -> Cinema API surrogate node: None Maxon API node: context_externaltimeinput -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 22186170048> Input port: context_externaltimeinput<searchpaths -> DescID: ((1936023922, 5, 0), (1667788897, 5, 0), (1953002240, 12, 0)) Input port: context_externaltimeinput<fps -> DescID: ((1718645504, 5, 0), (1, 19, 0)) Input port: context_externaltimeinput<time -> DescID: ((1953066341, 5, 0), (1, 19, 0)) Input port: context_externaltimeinput<nimbus -> DescID: ((1852403042, 5, 0), (1970470912, 12, 0)) Input port: context_externaltimeinput<ocioconfig -> DescID: ((1868786031, 5, 0), (1668247142, 5, 0), (1768357888, 12, 0)) Input port: context_externaltimeinput<renderspace -> DescID: ((1919250020, 5, 0), (1701999472, 5, 0), (1633903872, 12, 0)) Maxon API node: context_notime -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 16252169408> Input port: context_notime<searchpaths -> DescID: ((1936023922, 5, 0), (1667788897, 5, 0), (1953002240, 12, 0)) Input port: context_notime<fps -> DescID: ((1718645504, 5, 0), (1, 19, 0)) Input port: context_notime<time -> DescID: ((1953066341, 5, 0), (1, 19, 0)) Input port: context_notime<nimbus -> DescID: ((1852403042, 5, 0), (1970470912, 12, 0)) Input port: context_notime<ocioconfig -> DescID: ((1868786031, 5, 0), (1668247142, 5, 0), (1768357888, 12, 0)) Input port: context_notime<renderspace -> DescID: ((1919250020, 5, 0), (1701999472, 5, 0), (1633903872, 12, 0)) Maxon API node: builder -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 16252169792> Input port: builder<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: builder<in/flags -> DescID: ((1768828774, 5, 0), (1818322803, 12, 0)) Input port: builder<filter -> DescID: ((1718185076, 5, 0), (1701969920, 5, 0), (1, 133, 0)) Input port: builder/rot<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: builder/rot<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0)) Maxon API node: builder/rot -> Cinema API surrogate node: <c4d.BaseList2D object called Group with ID 300001078 at 22170201152> Input port: builder/rot<in -> DescID: ((1768816640, 5, 0), (1, 133, 0)) Input port: builder/rot<datatype -> DescID: ((1684108385, 5, 0), (1954115685, 5, 0), (1, 15, 0))Code
"""Demonstrates how to associate nodes in a Maxon API graph with their corresponding Cinema 4D API surrogate elements. Cinema 4D is split into two major APIs: - *Cinema API*: The 'classic' API that represents and describes most tangible entities in Cinema 4D, such as materials, objects, tags, and so on. This API is mostly based on the concept of `BaseList2D` scene elements that hold data containers and are organized in hierarchical and generic node relationships (via `GeListNode`, one of the base classes of `BaseList2D`). I.e., this data forms the graph that makes up a Cinema 4D scene, even when we usually think of it as a tree structure (but GeListNode relationships are more than pure tree relationships). - *Maxon API*: The Maxon API is a more modern API that also includes the Nodes API, which offers a a new (but not drop-in replacement) way to represent nodal scene data. It is used for Scene and Material Nodes at the moment (and subject of this part of the documentation). But the majority of the UI of Cinema 4D is still based on the Cinema API, and the Attribute Manager for example can only display `BaseList2D` scene elements and not `GraphNode` entities of the Maxon API. So, for user interaction purposes, Maxon API nodes must be associated with Cinema API surrogate scene elements that represent those nodes in the Cinema API world. A `NimusBaseInterface` is the glue between a Cinema API scene element and a Maxon API node graph. It not only provides access to the actual Nodes API graph associated with that element, but also manages the association between Nodes API nodes/ports and their Cinema API surrogate elements. This example focuses on the Scene Nodes system, but the same principles apply to other Maxon API node graphs. Compatibility Note: Remove all code in #main up to `print("\n\n--- Maxon API Scene Nodes Data ---\n") and the #mxutils import statement to make this example run in older versions of Cinema 4D (should work at least in 2025.x and with minor modifications even in 2024.x). """ __author__ = "Ferdinand Hoppe" __copyright__ = "Copyright (C) 2026 MAXON Computer GmbH" __date__ = "05/01/2026" __license__ = "Apache-2.0 License" __version__ = "2026.0.0" import c4d import maxon import mxutils doc: c4d.documents.BaseDocument # The currently active document. op: c4d.BaseObject | None # The primary selected object in `doc`. Can be `None`. def main() -> None: """Called by Cinema 4D when the script is being executed. """ # An good way to visualize what we are doing is mxutils.GetSceneGraphString, as it will give # us a visual representation of a Cinema API scene graph. We can find there the nodes we # will retrieve and associate with Maxon API nodes further below. You have to look for a # Scene Nodes scene hook in the output. It will also hold all surrogate nodes for the Maxon # API Scene Nodes graph of the document. print("--- Cinema API Scene Graph ---\n") c4d.ClearPythonConsole() print(mxutils.GetSceneGraphString(doc)) print("\n\n--- Maxon API Scene Nodes Data ---\n") # Now we attempt to get the Cinema API scene element to which the Scene Nodes system of a # document is tied (and which also physically holds all Cinema API surrogate nodes for the # Maxon API Scene Nodes graph of the document). For scene nodes, this is a scene hook, for # material graphs it would be a BaseMaterial. # # Scene hooks are a Cinema API node type for which always exactly one instance exists per # document. It is only a coincidence that they also use the term "scene" in their name, there # is no semantic relation between scene hooks and Scene Nodes. For material graphs, we would # for example call `FindNimbusRef` on the `BaseMaterial` instance instead of retrieving # a scene hook. hook: c4d.BaseList2D = doc.FindSceneHook(c4d.SCENENODES_IDS_SCENEHOOK_ID) if not hook: raise RuntimeError("Could not retrieve Scene Nodes scene hook.") # A `BaseList2D` offers various methods to retrieve `NimusBaseInterface` references for itself. # And a NimusBaseInterface is the glue between a Cinema API scene element and a Maxon API node # graph. Here is the connection being made between a Cinema API scene element in form of a # scene hook and the the Scene Nodes Maxon API graph that is associated with that scene hook. # Scene nodes come with the special condition that the their graph might not yet exist for # performance reasons, so we must always send #MSG_CREATE_IF_REQUIRED before attempting to # access a scene nodes graph. For a material node graph, this would not be necessary. hook.Message(maxon.neutron.MSG_CREATE_IF_REQUIRED) handler: maxon.NimbusBaseRef | None = hook.GetNimbusRef(maxon.NodeSpaceIdentifiers.SceneNodes) if not handler: raise RuntimeError("Could not retrieve Scene Nodes handler.") # Now we get the nodes graph that is associated with this nimbus handler and iterate over all # true nodes in it. The Nodes API follows the a bit odd notion that it represents graphs as # trees of entities, where each entity is a GraphNode. Some of those entities are 'true' nodes, # i.e., nodes that also an end user would see in the Node Editor, while other entities represent # things like input and output ports (but are also GraphNodes). So, in short, a GraphNode does # not necessarily represent a 'true' node. graph: maxon.NodesGraphModelRef = handler.GetGraph() root: maxon.GraphNode = graph.GetViewRoot() # For each entity in the graph... for entity in root.GetInnerNodes(maxon.NODE_KIND.ALL_MASK, False, None): # .. step over all non 'true node' entities ... if entity.GetKind() != maxon.NODE_KIND.NODE: continue # .. and find (or create) the BaseList2D Cinema API surrogate entity that represents the # current #entity in this Maxon API graph. This is the surrogate that is shown in an # Attribute Manager when the user selects the node in the Node Editor. Reading and writing # its parameters will be reflected in the Maxon API node and vice versa. surrogate: c4d.BaseList2D = handler.FindOrCreateCorrespondingBaseList(entity.GetPath()) print(f"Maxon API node: {entity.GetPath()} -> Cinema API surrogate node: {surrogate}") # Now we are going to iterate over all input ports of #entity and translate them into # parameter IDs for our #surrogate. for port in entity.GetInnerNodes(maxon.NODE_KIND.ALL_MASK, False, None): if port.GetKind() != maxon.NODE_KIND.INPORT: continue # The reasons why we use here a try/except block is because nodes tend to hold input # ports which only fulfill internal purposes and do not have a corresponding parameter # in the Cinema API surrogate node (ports without an UI). Getting the DescID for such # ports will fail with a ValueError because ports without an UI are not translated (and # we are also probably not interested in them here). try: did: c4d.DescID = handler.GetDescID(port.GetPath()) # This fails print(f"\tInput port: {port.GetPath()} -> DescID: {did}") except: pass if __name__ == '__main__': main() -
RE: How to change the Node spaces
Hello @gelobui,
Welcome to the Maxon developers forum and its community, it is great to have you with us!
Getting Started
Before creating your next postings, we would recommend making yourself accustomed with our forum and support procedures. You did not do anything wrong, we point all new users to these rules.
- Forum Overview: Provides a broad overview of the fundamental structure and rules of this forum, such as the purpose of the different sub-forums or the fact that we will ban users who engage in hate speech or harassment.
- Support Procedures: Provides a more in detail overview of how we provide technical support for APIs here. This topic will tell you how to ask good questions and limits of our technical support.
- Forum Features: Provides an overview of the technical features of this forum, such as Markdown markup or file uploads.
It is strongly recommended to read the first two topics carefully, especially the section Support Procedures: How to Ask Questions.
About your First Question
It depends a bit on how you mean your question. There is GetActiveNodeSpaceId which allows you to get the ID of the current node space. But there is no setting equivalent of that function. So, you cannot set a node space by its ID.
What you can do, is call the command which switches node spaces. These are however dynamically assigned and can have a different meaning, depending on how many render engines are installed. You can just check the script log after changing the space.
On this installation I have for example no extra render engines or node spaces installed, therefore Redshift is there
72000, 4.
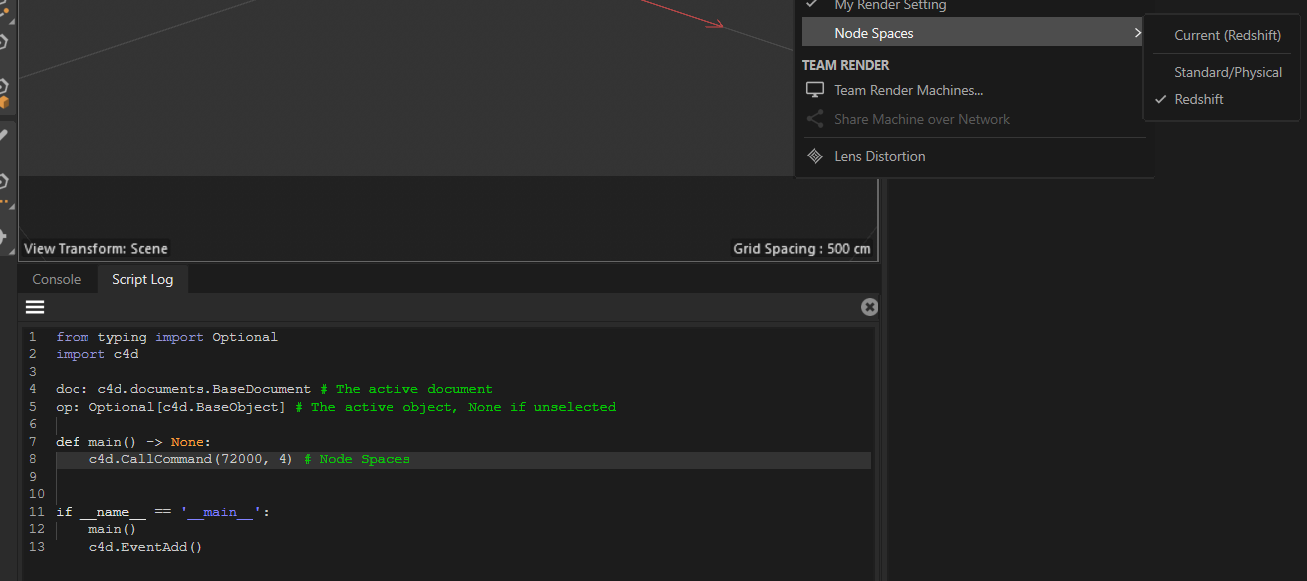
But on this machine I have the C++ SDK installed and therefore the
Examplenodes space, so Redshift is now72000, 5: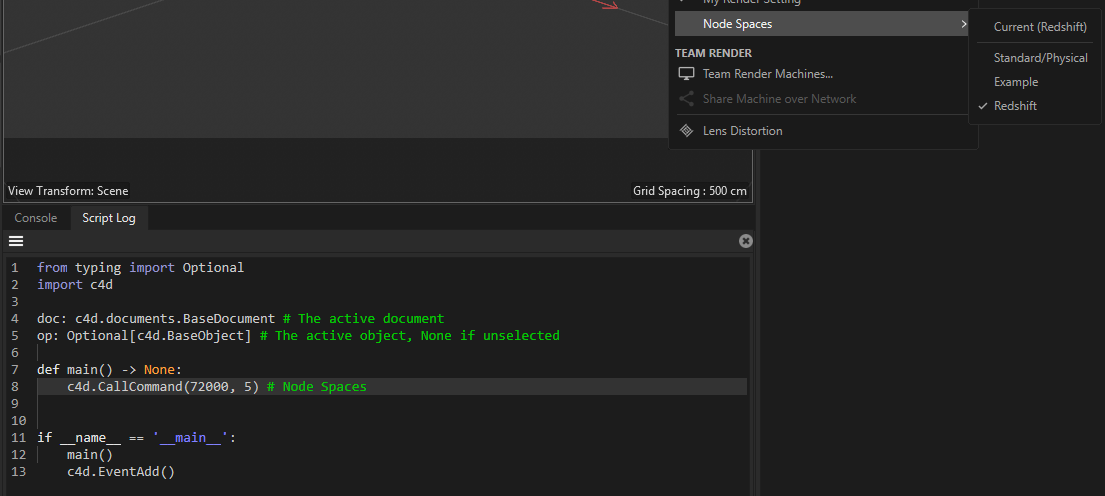
When you really want to do this in a fail safe manner, you would have to parse the menu of Cinema 4D to know with which sub-id to call
CallCommand.Cheers,
Ferdinand -
RE: ColorField/ColorDialog and GeUserArea – Color Space Questions
Hey @lasselauch,
Thank you for reaching out to us. The issue is likely that you do not respect OCIO color management in your document. You have marked this posting as
S26, but my hunch would be that you are using a newer version of Cinema 4D and an OCIO enabled document. The first implementation of OCIO showed up with S26 in Cinema 4D, although it was just some internal systems then such as the flagDOCUMENT_COLOR_MANAGEMENT_OCIOand user facing systems arrived with 2024 the earliest I think. In Python, you can only truly deal with this in 2025.0.0 and higher, as that is when we added the OCIO API to Python.When you indeed are testing this on an S26 or lower instance of Cinema 4D, the major question would be if
DOCUMENT_LINEARWORKFLOWis enabled or not. Because you cannot just blindly convert colors.Is this the intended behavior? Should we always convert LINEAR→sRGB when drawing colors from ColorField/ColorDialog in a GeUserArea?
The question would be what you consider here this ;). But if the question is if it is intended behavior for a scene with
DOCUMENT_COLOR_MANAGEMENT_BASICandDOCUMENT_LINEARWORKFLOWenabled, to have all its scene element and parameter colors expressed as sRGB 1.0, then yes, that is the major gist of the old linear workflow. It is also intended that drawing happens in sRGB 2.2 up this day.Issue 2: Eyedropper Roundtrip Doesn't Preserve Saturated Colors
Generally, multi question topics tend to become a mess (which is why we do not allow them). But in short: While roundtrips in the form of
sRGB 1.0 -> sRGB 2.2 -> sRGB 1.0are not absolutely lossless (you are always subject to floating point precision errors), there is no giant loss by default. I am not sure what mathTransformColoris using explicitly. A simplepow(color, 2.2)andpow(color, 1/2.2)are the naive way to do this and the loss would be rather small.TransformColormight be respecting tristimulus weights which is a bit more lossy but still in a small range.OCIO roundtrips on the other hand are generally quite lossy, because ACEScg is a very wide gamut color space and converting from ACEScg to sRGB 2.2 and back can lead to significant losses in saturated colors. Some conversion paths in OCIO are even irreversible in a certain sense (depending on what color spaces you have assigned to which transform). OCIO is rather complicated to put it mildly.
Is there a known issue with the ColorDialog eyedropper and color space conversion for saturated colors?
Not that I am aware of. But you likely just ignored OCIO. And while the default OCIO Render Space of Cinema 4D (ACEScg) is in a certain sense similar to sRGB 1.0 for low saturated colors, it diverges significantly for highly saturated colors. So, your loss of saturation is likely stemming from treating an OCIO document with an ACEScg render space as sRGB 1.0.
See also:
- Python OCIO Example: open_color_io_2025_2.py
- Python OCIO Example: py-ocio_node_2025.pyp
- C++ Manual: Color Management
- C++ Manual: OCIO
Last but not least, I attached an example of what you are trying to achieve, get a color from a color gadget in a dialog and draw with it faithfully in your own user area.
Cheers,
Ferdinand"""Demonstrates how to correctly draw with OCIO colors in a dialog. This examples assumes that you are using Cinema 4D 2025+ with an OCIO enabled document. It will also work in other versions and color management modes, but the point of this example is to demonstrate OCIO color conversion for drawing in dialogs (more or less the same what is already shown in other OCIO examples in the SDK). """ import c4d from c4d import gui class ColorArea(gui.GeUserArea): """Draws a color square in a custom UI element for a dialog. """ def __init__(self): self._color: c4d.Vector = c4d.Vector(1, 0, 0) # The color to draw, this is in sRGB 2.2 def GetMinSize(self): return 75, 20 def DrawMsg(self, x1: int, y1: int, x2: int, y2: int, msg: c4d.BaseContainer) -> None: """Draw the color of the area. """ self.OffScreenOn() # Draw the color. self.DrawSetPen(self._color) self.DrawRectangle(x1, y1, x2, y2) class ColorDialog(gui.GeDialog): """Implements a dialog that hosts a color field and chooser as well as our custom color area. The colors in the color field and chooser are in render space, so we have to convert them to sRGB for correct display in our user area. All three color widgets are kept in sync, i.e., changing one updates the others. """ ID_DUMMY_ELEMENT: int = 1000 ID_COLOR_CHOOSER: int = 1001 ID_COLOR_FIELD: int = 1002 ID_COLOR_AREA: int = 1003 SPACING_BORDER: int = (5, 5, 5, 5) SPACING_ELEMENTS: int = (5, 5) DEFAULT_FLAGS: int = c4d.BFH_SCALEFIT | c4d.BFV_SCALEFIT def __init__(self) -> None: """Initializes the dialog. """ # Reinitializing the color area each time CreateLayout is called, could cause loosing its # state when this is an async dialog docked in the UI and part of a layout, as CreateLayout # can be called more than once when a dialog must be reinitialized on layout changes. So, # doing it in __init__ or guarding it with a check if it is already created in CreateLayout # is better. self._color_area: ColorArea = ColorArea() def CreateLayout(self) -> None: """Called by Cinema 4D to populate the dialog with elements. """ self.SetTitle("Dialog Color OCIO Demo") # Using the same ID for dummy elements multiple times is fine, using IDs < 1000 is often # not a good idea, as Cinema 4D usually operates in that range, and therefore an ID such # as 0 can lead to issues (0 is AFIAK not actually used but better safe than sorry). if self.GroupBegin(self.ID_DUMMY_ELEMENT, self.DEFAULT_FLAGS, cols=1): self.GroupBorderSpace(*self.SPACING_BORDER) self.GroupSpace(*self.SPACING_ELEMENTS) # Add a color chooser and a color field. self.AddColorChooser(self.ID_COLOR_CHOOSER, c4d.BFH_LEFT) self.AddColorField(self.ID_COLOR_FIELD, c4d.BFH_LEFT) # Add our user area to display the color. self.AddUserArea(self.ID_COLOR_AREA, c4d.BFH_LEFT) self.AttachUserArea(self._color_area, self.ID_COLOR_AREA) self.GroupEnd() return True def InitValues(self) -> bool: """Called by Cinema 4D to initialize the dialog values. """ self.SetColors(c4d.Vector(1, 0, 0)) return True def SetColors(self, color: c4d.Vector, doc: c4d.documents.BaseDocument | None = None) -> None: """Sets the colors of all color widgets to the given render space #color. """ # Just set the two color widgets first, as they expect render space colors. self.SetColorField(self.ID_COLOR_CHOOSER, color, 1.0, 1.0, c4d.DR_COLORFIELD_NO_BRIGHTNESS) self.SetColorField(self.ID_COLOR_FIELD, color, 1.0, 1.0, c4d.DR_COLORFIELD_NO_BRIGHTNESS) # When the call did not provide a document, use the active document. if not isinstance(doc, c4d.documents.BaseDocument): doc = c4d.documents.GetActiveDocument() # Check in which color mode the document is. Explicit OCIO color management exists in this # form since S26 but it really only took off with 2025. isOCIO: bool = False if (c4d.GetC4DVersion() >= 2025000 and doc[c4d.DOCUMENT_COLOR_MANAGEMENT] == c4d.DOCUMENT_COLOR_MANAGEMENT_OCIO): # All colors in a document are render space colors (including the color fields in # dialogs). GUI drawing however still happens in sRGB space, so we need to convert # the render space color to sRGB for correct display. For that we need a document # because it contains the OCIO config and the converted which is derived from it. converter: c4d.modules.render.OcioConverter = doc.GetColorConverter() # Transform a render space color to sRGB space (there are other conversion paths # too, check the docs/examples on OCIO). color: c4d.Vector = converter.TransformColor( color, c4d.COLORSPACETRANSFORMATION_OCIO_RENDERING_TO_SRGB) isOCIO = True elif not isOCIO and doc[c4d.DOCUMENT_LINEARWORKFLOW]: # For non-OCIO documents (older than S26 or DOCUMENT_COLOR_MANAGEMENT_BASIC), the scene # element color space ('render space' in OCIO terms) can either be sRGB 2.2 or sRGB 1.0 # (linear sRGB), depending on whether DOCUMENT_LINEARWORKFLOW is set or not. In that # case, we would have to convert from gamma 1.0 to 2.2. In a modern OCIO document, we # could also use #converter for this, but for legacy reasons I am using here the old # c4d.utils function. It might be better to use the converter when this is a 2025+ # instance of Cinema 4D. #DOCUMENT_LINEARWORKFLOW is really old, it exists at least # since #R21 (I did not check earlier versions), so I am not doing another version check. color = c4d.utils.TransformColor(color, c4d.COLORSPACETRANSFORMATION_LINEAR_TO_SRGB) # Last but not least, in practice you would probably encapsulate this logic in your user # area, similarly to how native color elements operate just in Render Space but draw in # sRGB space. For dialogs (compared to description parameters), this is a bit complicated # by the fact that one cannot unambiguously associate a dialog with a document from which # to take the color management settings. A custom GUI of a description parameter can # always get the node it is hosted by and its document. For dialog GUIs that is not possible. # So, we have to do the active document approach I showed here. # In a super production scenario, you would overwrite CoreMessage() of the user area or # dialog, to catch the active document changing, to then update the color conversion, as # with the document change, also the OCIO config could changed and with that its render # space transform. # # All in all probably a bit overkill, and I would ignore this under the banner of "who # cares, just reopen the dialog and you are fine". Because users will also rarely change # the default render space transform of ACEScg to something else. self._color_area._color = color self._color_area.Redraw() def Command(self, id: int, msg: c4d.BaseContainer) -> bool: """Called by Cinema 4D when the user interacts with a dialog element. """ if id == self.ID_COLOR_CHOOSER: color: c4d.Vector = self.GetColorField(self.ID_COLOR_CHOOSER)["color"] self.SetColors(color) elif id == self.ID_COLOR_FIELD: color: c4d.Vector = self.GetColorField(self.ID_COLOR_FIELD)["color"] self.SetColors(color) return True # Please do not do this hack in production code. ASYNC dialogs should never be opened in a Script # Manager script like this, because this will entail a dangling dialog instance. Use modal dialogs # in Script Manager scripts or implement a plugin such as a command to use async dialogs. dlg: ColorDialog = ColorDialog() if __name__ == '__main__': dlg.Open(c4d.DLG_TYPE_ASYNC, defaultw=480, defaulth=400) -
RE: ObjectData handles - Unexpected position jitter
I now also see that my example is buggy in the perspective view (and other views I have not implemented). For these cases you would have to do exactly what I did in my
ohandlenullexample, project the point into a plane placed on the origin of the object with a normal that is the inverse of the camera normal.Given that this also affects internal code, it is quite likely that we will fix this. If I were you, I would just keep my old code and ignore this very niche edge case. When you really want this to work you would have to implement
MoveHandleand handle the different view projections of Cinema 4D. This can probably be done in 50-100 lines of code or so, but it would be something I would try to avoid doing, as viewport projections can be tricky to handle. -
RE: ObjectData handles - Unexpected position jitter
Hey @PixelsInProgress,
so, I had a look. First of all, I came up with reproduction steps which you were lacking (see our Support Procedures). It is important to provide these, because when you just provide a 'sometimes it works, sometimes it doesn't' or a 'it is hard to reproduce' the risk is high, that I or Maxime will just declare something non-reproducible and move on (which almost happened here). We understand this is extra work and that you already put work into boiling down the issue, but it is in your own interest to be more precise with reproduction steps.
I am not 100% sure if we will consider this a bug, because I do not yet fully understand why this happens, but I have moved this into bugs for now. I also provide a workaround based on
MoveHandleas already hinted at before.Edit: Since this bug also affects objects provided by Cinema 4D, such as a cloner in linear mode or the field force object, this is now a Cinema 4D and not SDK bug anymore.
Issue
ObjectData.SetHandlecode can lead to jitter issues when usingHANDLECONSTRAINTTYPE_FREE.Reproduction
- Add the example object plugin to a scene.
- Switch to a two panel viewport layout, make the right panel a "Right" projection, the left panel a "Top" projection.
- Give the object a non-default transform.
- Interact with the handle in one of the panels.
- Now move the object in that panel.
- Interact with the handle in the other panel.
Result
- The handle jitters between the world plane perpendicular to the other view and the 'correct' position.
Code
import c4d PLUGIN_ID = 1067013 PIP_HANDLE_EXAMPLE_POSITION = 1000 PIP_HANDLE_EXAMPLE_GROUP_STORAGE_GROUP = 2000 PIP_HANDLE_EXAMPLE_CONTAINER_INTERNAL_CONTAINER = 3000 class PIP_HandleExample(c4d.plugins.ObjectData): def Init(self,op,isCloneInit): self.InitAttr(op, c4d.Vector, c4d.PIP_HANDLE_EXAMPLE_POSITION) if not isCloneInit: op[c4d.PIP_HANDLE_EXAMPLE_POSITION] = c4d.Vector(0,0,0) return True def GetHandleCount(self, op): return 1 def GetHandle(self, op, i, info): info.position = op[c4d.PIP_HANDLE_EXAMPLE_POSITION] info.type = c4d.HANDLECONSTRAINTTYPE_FREE def SetHandle(self, op, i, p, info): op[c4d.PIP_HANDLE_EXAMPLE_POSITION] = p def Draw(self, op, drawpass, bd, bh): if drawpass != c4d.DRAWPASS_HANDLES: return c4d.DRAWRESULT_SKIP bd.SetMatrix_Matrix(op, op.GetMg()) bd.SetPen(c4d.GetViewColor(c4d.VIEWCOLOR_HANDLES)) info = c4d.HandleInfo() self.GetHandle(op, 0, info) bd.DrawHandle(info.position, c4d.DRAWHANDLE_BIG, 0) return c4d.DRAWRESULT_OK if __name__ == "__main__": if not c4d.plugins.RegisterObjectPlugin( id=PLUGIN_ID, str="PIP - Handle example", g=PIP_HandleExample, description="PIP_HandleExample", icon=None, info=c4d.OBJECT_GENERATOR): raise RuntimeError("Failed to register PIP_HandleExample plugin.")Workaround
As already hinted at, you can override
MoveHandleinstead ofSetHandleto implement your own handle movement logic. This way you have full control over how the mouse position is interpreted and can work around the jitter issue. See below for an example implementation.Files: PIP_HandleExample.zip
# def SetHandle(self, op, i, p, info): # """ Not required as we override MoveHandle. # """ # op[c4d.PIP_HANDLE_EXAMPLE_POSITION] = p def MoveHandle(self, op: c4d.BaseObject, undo: c4d.BaseObject, mouse_pos: c4d.Vector, hit_id: int, qualifier: int, bd: c4d.BaseDraw) -> bool: """Called by Cinema 4D when the user interacts with a handle. """ # Get the mouse position in world space and then convert it to object space. The issue # of this solution is that it will project the point down to one of the world planes ( # the plane to which the the #SetHandle code jitters). So, the axis which is perpendicular # to the view plane will be zeroed out. worldMousePos: c4d.Vector = bd.SW(mouse_pos) localMousePos: c4d.Vector = ~op.GetMg() * worldMousePos # To fix that, we must project the point into a plane we consider correct. You could do this # brutishly by for example checking the projection of #bd and then just align the component # of #worldMousePos that is perpendicular to that plane. You could also add some 'carry on' # logic here which respects previous data, but I didn't do that. projection: int = bd[c4d.BASEDRAW_DATA_PROJECTION] if projection in (c4d.BASEDRAW_PROJECTION_TOP, c4d.BASEDRAW_PROJECTION_BOTTOM): worldMousePos.y = op.GetMg().off.y elif projection in (c4d.BASEDRAW_PROJECTION_FRONT, c4d.BASEDRAW_PROJECTION_BACK): worldMousePos.z = op.GetMg().off.z elif projection in (c4d.BASEDRAW_PROJECTION_LEFT, c4d.BASEDRAW_PROJECTION_RIGHT): worldMousePos.x = op.GetMg().off.x op[c4d.PIP_HANDLE_EXAMPLE_POSITION] = ~op.GetMg() * worldMousePos return TrueCheers,
Ferdinand -
RE: ObjectData handles - Unexpected position jitter
Well, what I meant with feedback loop, is that you never constraint your data in any shape or form. All code examples and internal code work like this:
def GetHandle(self, op, i, info): info.position = self.handle_position # or op[c4d.ID_INTERNAL_HANDLE_STORAGE] info.type = c4d.HANDLECONSTRAINTTYPE_SOMETYPE info.direction = Vector(...) def SetHandle(self, op, i, p, info): self.handle_position = Clamp(p)I.e., here
Clampis called onpbefore it is fed back intohandle_position. In my bezier handle example I usedMoveHandleto project the current mouse pick point into the plane where I wanted to have it. You could also do the same inSetHandle. The viewport picking algorithm has no idea where you consider to be the 'correct' working plane. It does its best to guess, but you must still check and or help.I haven't had a look at your code yet, will do next week (hopefully on Monday). It could be that there is a bug in the Python API, but that unbound nature of your code does strike me as incorrect.
Cheers,
Ferdinand -
RE: ObjectData handles - Unexpected position jitter
Hey @PixelsInProgress,
thank you for reaching out to us. That is not possible to answer like this, please provide an executable code example of what you are doing.
I guess the the reason for your problems are that you use the a bit niche constraint type
HANDLECONSTRAINTTYPE_FREEand create a transform feedback loop when you feed your own user data into your handle without constraining that data. Keep in mind that handle code is called view-based. You might have to implementMoveHandleto correctly transform your point. But I have no idea what you are trying to do, so I am mostly guessing.I have written a while ago this C++ code example which implements a camera dependent handle, which might be what you are trying to do here.
Cheers,
Ferdinand -
RE: Educational Licenses
No one might see this here, as notifications are currently broken, but there is an all new licensing manual and example in the SDK which should answer the questions asked here. Feel free to follow up, in case something remains unclear.
-
Maxon One 2026.1 SDK Release
Dear development community,
On December the 3rd, 2025, Maxon Computer unveiled Maxon One 2026.1 in its December release. For an overview of the new features please refer to the news posting.
Alongside this release, existing APIs have been updated. For a detailed overview, please see the Cinema 4D C++ SDK, the Cinema 4D Python SDK, and ZBrush Python SDK change notes.
Cinema 4D
C++ API
- Only minor API changes have been made.
Python API
- Added new manual and code example revolving around plugin licening.
- Minor bug fixes in older code examples.
ZBrush
Python API
- Finalized the ZBrush SDK, with new manuals, code examples, and an all new SDK look.
- Added new ZBrush-Python-API-Examples repository on Github.
Head to our download section to grab the newest SDK downloads.
Happy rendering and coding,
the Maxon SDK Team We are aware that the notifications are currently malfunctioning on the forum.
We are aware that the notifications are currently malfunctioning on the forum.
 Cloudflare unfortunately still does interfere with our server cache. You might have to refresh your cache manually to see new data when you read this posting within 24 hours of its release.
Cloudflare unfortunately still does interfere with our server cache. You might have to refresh your cache manually to see new data when you read this posting within 24 hours of its release.