Hi @chuanzhen ,
Please note that according to our Support Procedures your question lies out of the scope of our support as it is solely an algorithmic question.
Regarding your question. There're so many open questions in your problem statement that directly affect the path you're going to follow. Hence, I will first try to ground at least some of them and then we'll see how it can be extended to your more complex scenario if there's a need for that. Feel free to elaborate on your question on a higher scale, if my thoughts go in a wrong direction.
First, let's assume your quadrilateral is actually a parallelogram (i.e. 1. lives in 2D-space; 2. opposite sides are parallel). That's quite a strong assumption, but we'll get back to it later. Then instead of having a line that intersects point P, we can think of it as a point P_ab on the line AB (because from that your can easily reconstruct your line as it will be parallel to the side lines).
Simplified case with parallelogramm:
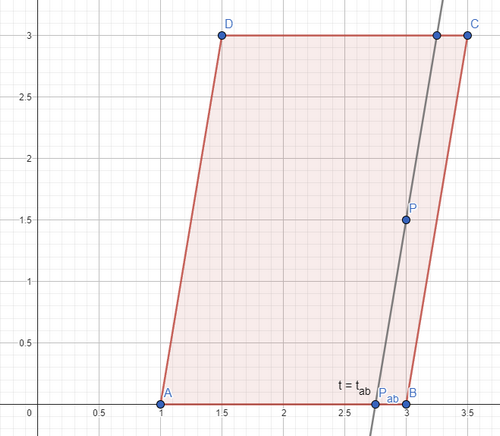
Let's then instead working in a 2D space (i.e. working with point P_ab), simplify it further and use the corresponding single value 0.0 <= t_ab <= 1.0, considering that your line AB is defined as f(t) = A + t * (B - A), where t = [0...1], A and B were originally in R^2 (2-component vectors), but since we only work on the line AB, we can consider them being in R (and then will convert them back to R^2 using original points A and B in 2D space).
If you look at it now, we've reduced the task to the 1D space, where we have interval from 0.0 to 1.0 and some point t_ab in between that corresponds to your initial point P. Let's also for now consider interval [0...100] instead of [0...1], and let's for now consider only integral numbers on this interval, just for the sake of simplicity.
If we now get back to your original question, with this 1D space problem scope it was reduced to a simple task of searching for the greatest common divisor (GCD) between the two numbers: t_ab and 100. By the way, I assume here that you're looking for the greatest number that would satisfy your problem statement, because number 1 would always be a correct answer as well as some other numbers that are integral divisors of t_ab and 100). Additionally we can quickly make one small optimization step according to the euclidean algorithm and look for t_x = gcd(t_ab, 100 - t_ab) instead.
Generally speaking that's already the answer you were looking for, but here the interesting part begins. The biggest issue that you have here is the space your numbers are in. It's working just fine in Z (integers), but how do you handle R (real numbers)? Depending on your desired precision the task can be quite expensive for processing. I didn't do any reasearch about it, but the naive way would be to simply make a lossy conversion from R to Z and then back to R (although there might exist some interesting tricks for that).
Let's get back to our 0.0 <= t_ab <= 1.0 now. In this case, the easy way would be to scale t_ab to some big value and work with it in Z, e.g.
t_x = gcd(t_ab * 10000, (1 - t_ab) * 10000) / 10000.0
Since you now have t_ab, you can find back P_ab that lies on segment AB. For that you just need to apply your AB formula:
{P_ab}_k = A + k * t_x * (B - A)
, where k runs from 0 to N = 1.0 / t_x, and {P_ab}_k here is a set of points that lie on line AB. The only remaining step is to get your desired lines that are parallel to side lines AD and BC and go through the set {P_ab}. That was the simplified problem.
What'd happen now if we have an arbitrary quadrilateral? Actually, the core calculation would stay the same, the only issue would be to find t_ab, because the side lines are not parallel anymore. In this case, I think the easiest way would be to find a perspective transform M from your arbitrary quadrilateral ABCD to something that is easier to work with, e.g. a unit square A'B'C'D'. Once found, you just apply this transform to your original point p: p' = M * p and continue the same route as described with the parallelogram, because square also has parallel side lines.
Arbitrary quadrilateral:

Perspective transform:

Getting another step back to your original question and extending this approach further to 3D shouldn't be a problem, as you just need to transform your arbitrarily placed quadrilateral such that it is aligned with your coordinate system basis before doing any of the above mentioned calculations. For that you'd need to calculate cross product on 2 adjacent edges of your quadrilateral, make this basis orthonormal and transform coordinates to this new basis.
In case you also like to cover scenario with non-planar quadrilateral you would likely need to use some imagination for that. At least then the 'perspective transform' trick wouldn't work anymore and you would need to go into all the depths of solving the optimization problem for the minimal distance to your point P.
Please note that there's a convenient GeometryUtilsInterface that contains lots of useful implementations. For example,
Barycentric Coordinates functions will be helpful for the 'perspective transform' part
Projection functions will help you jumping between R^3 and R^2
Cheers,
Ilia