Dear developers,
My name is Ilia Mazlov, I joined Maxon SDK Team recently. I'm hoping to be seamlessly integrating to the community and be helpful bringing knowledge and experience I got in the Exchange Team.
I'm looking forward to working with you! 
Cheers,
Ilia
Hi James,
Thank you for your follow up message. The information about what you're trying to achieve is still missing or highly implicit in your reply (there is no question).
Assuming your goal is to adjust shader attributes (color value for color shader and bitmap path for the bitmap shader), the snippet on the thread that I pointed you out to shows up exactly this case (for the bitmap path): How to change bitmap in layered shader?. I've sketched up the corresponding part for the color shader for you (please find below).
The c4d.LAYER_S_PARAM_SHADER_LINK parameter basically points to the object that contains the shader. Please, refer to the C++ documentation in this regard: LAYER_S_PARAM_SHADER. Some parts of our API are better documented on the C++ side, so it is worth double checking the missing parts there.
Cheers,
Ilia
The code snippet:
import c4d
doc: c4d.documents.BaseDocument # The active document
def RetrieveShader(layer: c4d.LayerShaderLayer):
# Check if the layer is really a shader
if not layer or layer.GetType() != c4d.TypeShader:
raise ValueError("Layer is not a shader")
# Retrieve the linked shader of this layer
return layer.GetParameter(c4d.LAYER_S_PARAM_SHADER_LINK)
def ChangeTexturePathOfLayer(layer: c4d.LayerShaderLayer, texturePath: str) -> None:
"""Change the texture path of an existing Bitmap Layer
"""
shader: c4d.C4DAtom = RetrieveShader(layer)
# check if this is really a bitmap shader
if not shader.CheckType(c4d.Xbitmap):
raise ValueError("First layer is not a bitmap shader")
# Update the texture path of the shader linked to this layer
shader[c4d.BITMAPSHADER_FILENAME] = texturePath
def ChangeColorShader(layer: c4d.LayerShaderLayer, color: c4d.Vector) -> None:
"""Change the color of and existing Color Shader
"""
shader: c4d.C4DAtom = RetrieveShader(layer)
if not shader.CheckType(c4d.Xcolor):
raise ValueError("First layer is not a color shader")
shader[c4d.COLORSHADER_COLOR] = color
def main() -> None:
# Get the color channel shader for the first material in the scene.
material: c4d.BaseMaterial | None = doc.GetFirstMaterial()
if not material:
raise RuntimeError("Please add at least one material to the document.")
shader: c4d.BaseList2D | None = material.GetFirstShader()
if not shader or not shader.CheckType(c4d.Xlayer):
raise RuntimeError("First shader is not a layer shader")
# Update an existing Bimtap Layer
ChangeTexturePathOfLayer(shader.GetFirstLayer(), r"D:\temp\tex2.jpg")
# Update an existing Color Layer
ChangeColorShader(shader.GetFirstLayer().GetNext(), c4d.Vector(0., 1., 0.))
c4d.EventAdd()
if __name__ == '__main__':
main()
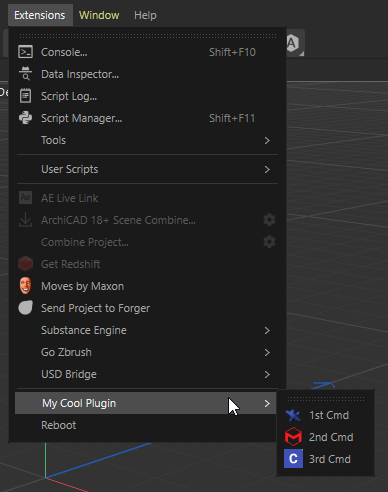
Hi @chuanzhen ,
Please note that according to our Support Procedures your question lies out of the scope of our support as it is solely an algorithmic question.
Regarding your question. There're so many open questions in your problem statement that directly affect the path you're going to follow. Hence, I will first try to ground at least some of them and then we'll see how it can be extended to your more complex scenario if there's a need for that. Feel free to elaborate on your question on a higher scale, if my thoughts go in a wrong direction.
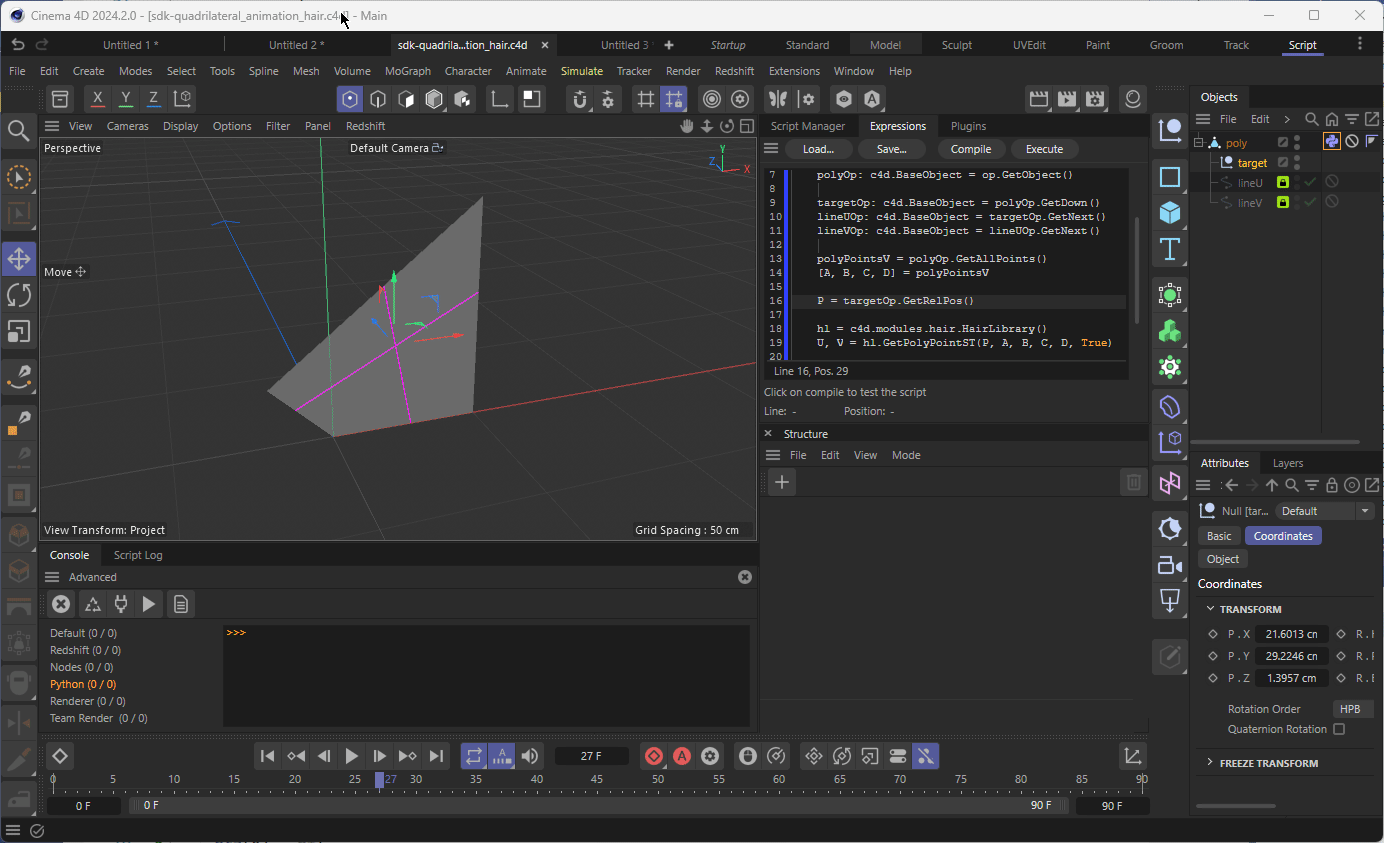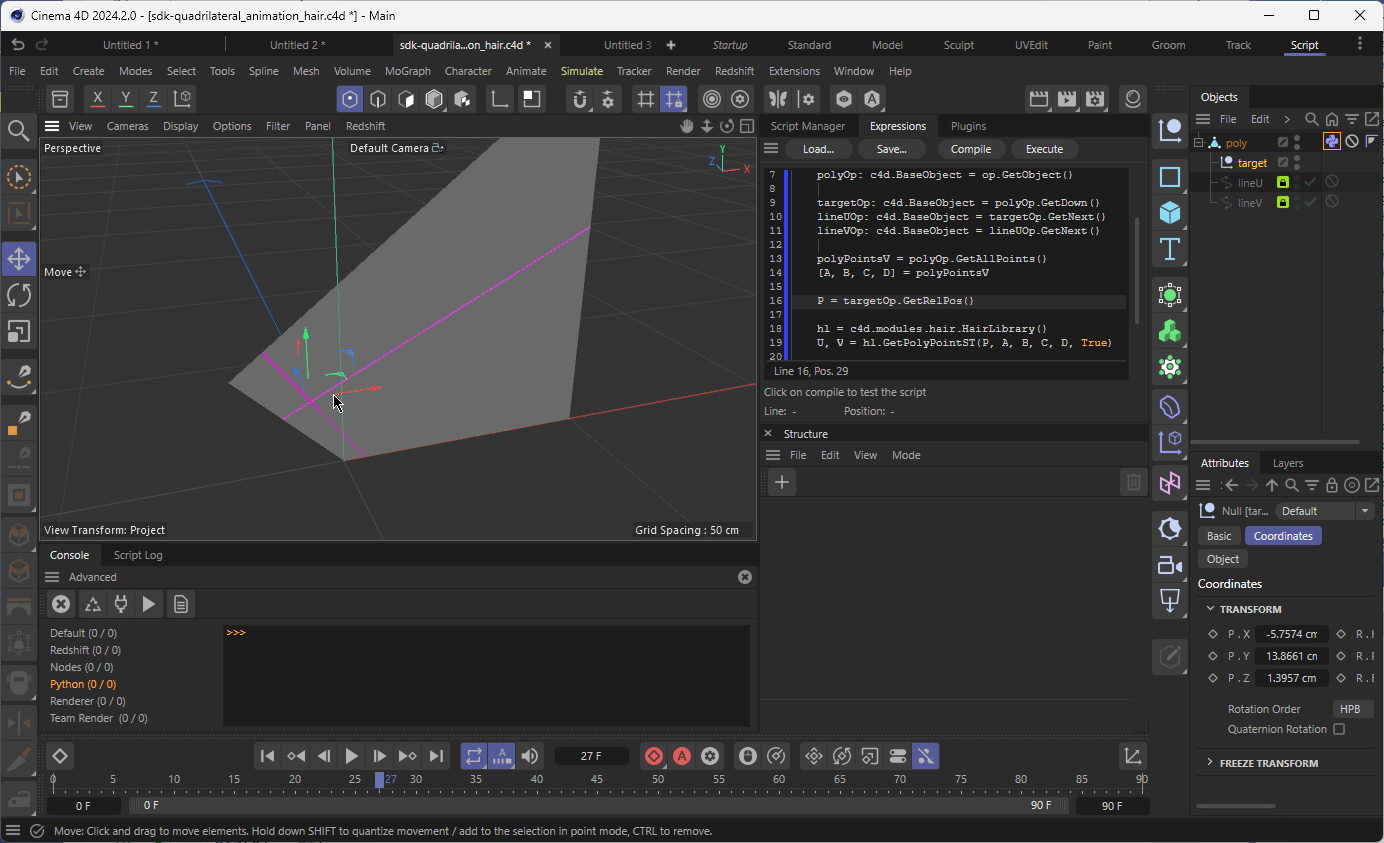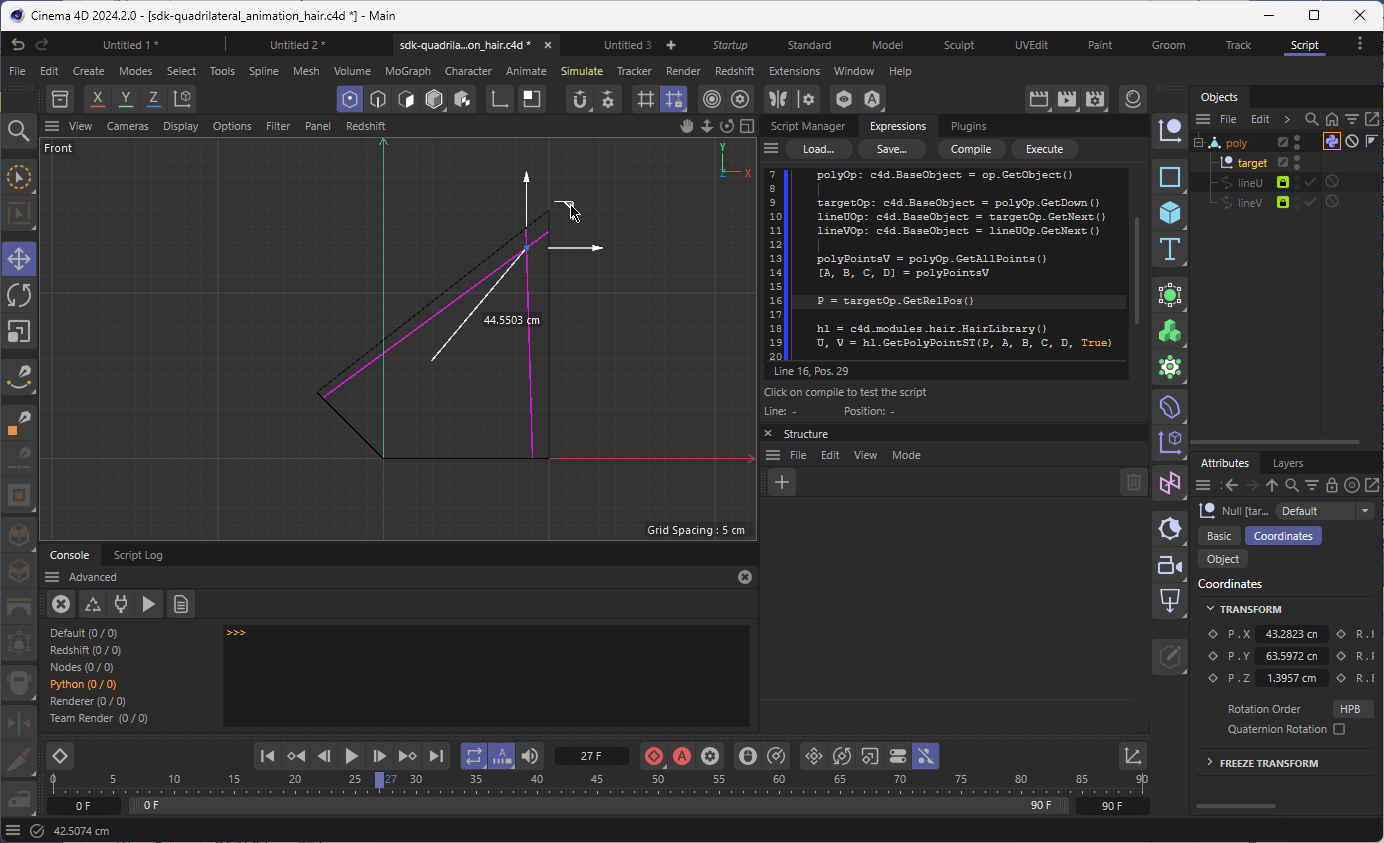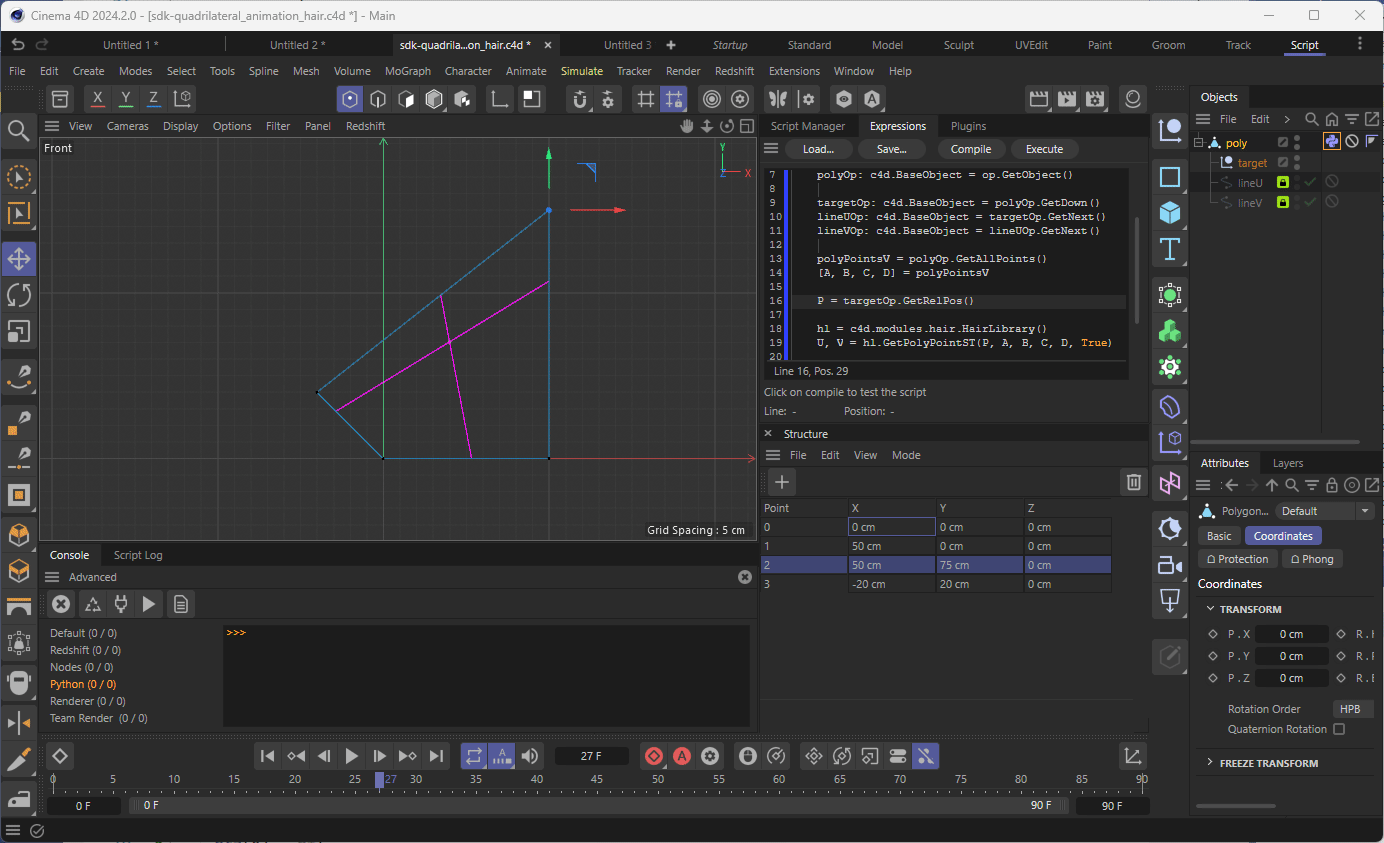
First, let's assume your quadrilateral is actually a parallelogram (i.e. 1. lives in 2D-space; 2. opposite sides are parallel). That's quite a strong assumption, but we'll get back to it later. Then instead of having a line that intersects point P, we can think of it as a point P_ab on the line AB (because from that your can easily reconstruct your line as it will be parallel to the side lines).
Simplified case with parallelogramm:
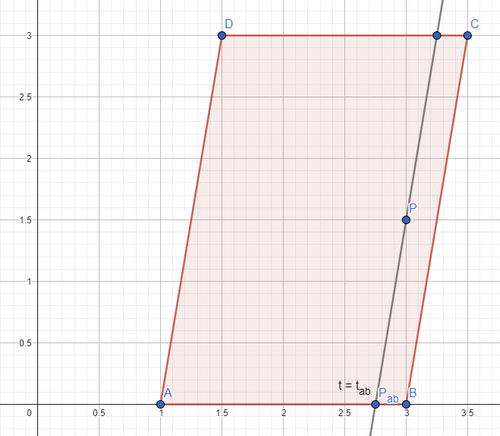
Let's then instead working in a 2D space (i.e. working with point P_ab), simplify it further and use the corresponding single value 0.0 <= t_ab <= 1.0, considering that your line AB is defined as f(t) = A + t * (B - A), where t = [0...1], A and B were originally in R^2 (2-component vectors), but since we only work on the line AB, we can consider them being in R (and then will convert them back to R^2 using original points A and B in 2D space).
If you look at it now, we've reduced the task to the 1D space, where we have interval from 0.0 to 1.0 and some point t_ab in between that corresponds to your initial point P. Let's also for now consider interval [0...100] instead of [0...1], and let's for now consider only integral numbers on this interval, just for the sake of simplicity.
If we now get back to your original question, with this 1D space problem scope it was reduced to a simple task of searching for the greatest common divisor (GCD) between the two numbers: t_ab and 100. By the way, I assume here that you're looking for the greatest number that would satisfy your problem statement, because number 1 would always be a correct answer as well as some other numbers that are integral divisors of t_ab and 100). Additionally we can quickly make one small optimization step according to the euclidean algorithm and look for t_x = gcd(t_ab, 100 - t_ab) instead.
Generally speaking that's already the answer you were looking for, but here the interesting part begins. The biggest issue that you have here is the space your numbers are in. It's working just fine in Z (integers), but how do you handle R (real numbers)? Depending on your desired precision the task can be quite expensive for processing. I didn't do any reasearch about it, but the naive way would be to simply make a lossy conversion from R to Z and then back to R (although there might exist some interesting tricks for that).
Let's get back to our 0.0 <= t_ab <= 1.0 now. In this case, the easy way would be to scale t_ab to some big value and work with it in Z, e.g.
t_x = gcd(t_ab * 10000, (1 - t_ab) * 10000) / 10000.0
Since you now have t_ab, you can find back P_ab that lies on segment AB. For that you just need to apply your AB formula:
{P_ab}_k = A + k * t_x * (B - A)
, where k runs from 0 to N = 1.0 / t_x, and {P_ab}_k here is a set of points that lie on line AB. The only remaining step is to get your desired lines that are parallel to side lines AD and BC and go through the set {P_ab}. That was the simplified problem.
What'd happen now if we have an arbitrary quadrilateral? Actually, the core calculation would stay the same, the only issue would be to find t_ab, because the side lines are not parallel anymore. In this case, I think the easiest way would be to find a perspective transform M from your arbitrary quadrilateral ABCD to something that is easier to work with, e.g. a unit square A'B'C'D'. Once found, you just apply this transform to your original point p: p' = M * p and continue the same route as described with the parallelogram, because square also has parallel side lines.
Arbitrary quadrilateral:
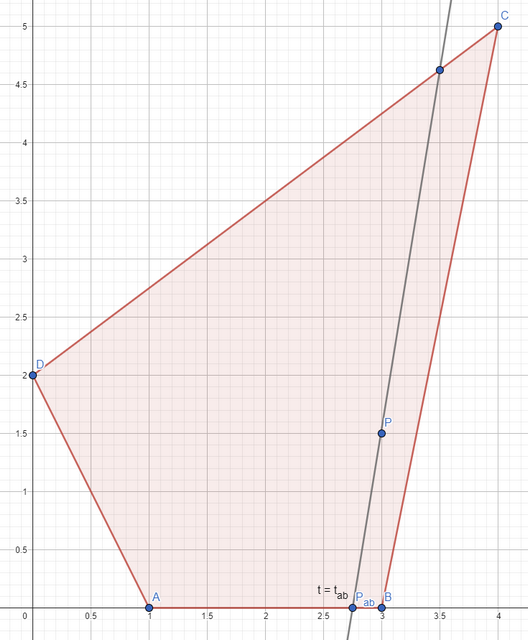
Perspective transform:
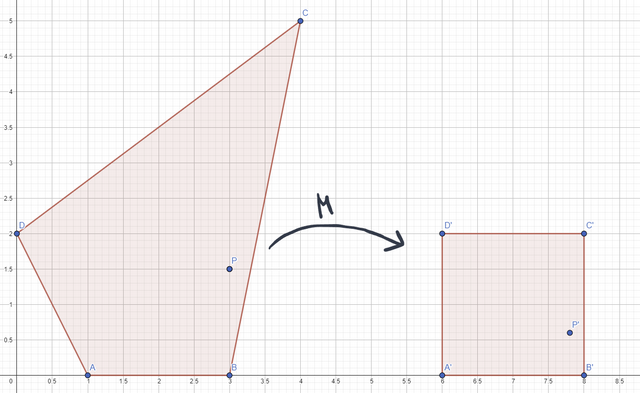
Getting another step back to your original question and extending this approach further to 3D shouldn't be a problem, as you just need to transform your arbitrarily placed quadrilateral such that it is aligned with your coordinate system basis before doing any of the above mentioned calculations. For that you'd need to calculate cross product on 2 adjacent edges of your quadrilateral, make this basis orthonormal and transform coordinates to this new basis.
In case you also like to cover scenario with non-planar quadrilateral you would likely need to use some imagination for that. At least then the 'perspective transform' trick wouldn't work anymore and you would need to go into all the depths of solving the optimization problem for the minimal distance to your point P.
Please note that there's a convenient GeometryUtilsInterface that contains lots of useful implementations. For example,
Barycentric Coordinates functions will be helpful for the 'perspective transform' part
Projection functions will help you jumping between R^3 and R^2
Cheers,
Ilia
Hello @aghiad322,
Welcome to the Plugin Café forum and the Cinema 4D development community, it is great to have you with us!
Before creating your next postings, we would recommend making yourself accustomed with our Forum and Support Guidelines, as they line out details about the Maxon SDK Group support procedures. Of special importance are:
There's a great example script that reveals how to work with instance object.
Regarding your exact scenario, you have to insert the referenced object to the document as well. You can check the following code snippet:
import c4d
doc: c4d.documents.BaseDocument # The active document
def main() -> None:
objCube = c4d.BaseList2D(5159)
objInstance = c4d.InstanceObject()
objInstance.SetReferenceObject(objCube)
# objInstance = c4d.BaseList2D(5126)
# objInstance[c4d.INSTANCEOBJECT_LINK] = objCube
doc.InsertObject(objInstance)
doc.InsertObject(objCube)
if __name__ == '__main__':
main()
Note, commented out you find an equivalent way to create and setup up instance object.
Cheers,
Ilia
Hi @chuanzhen ,
Sorry for the delayed answer.
I've just realized that perspective transform conversion that I've suggested to you earlier isn't going to work here, as it is not an affine transform, hence it doesn't preserve ratios on edges (and preservation of collinearity is not enough in your case).
However, once I had a fresh look at the problem here, I've also realized that even if some transform M would have worked here, it would have been such an overkill for this problem. What you're actually looking for is just a UV coordinates of your point P' that lies inside of an arbitrary quadrilateral, so there's even no need to transform anything here.
When you have your ABCD quadrilateral defined in R^3 space and some point Q' = <u, v>, defined in R^2: 2D plane of this quadrilateral, then you can find your point P' (defined in R^3) by doing a bilinear interpolation along edges of your quadrilateral. However, in your case you need to solve the inverse problem, when you have your P' and would like to find Q'. This is as easy as solving a properly defined quadratic equation on v (or u, doesn't really matter).
Luckily you can use CalculatePolygonPointST() in C++ (or GetPolyPointST() in Python) exactly for that. Please find attached scene that demonstrates exactly this.
Cheers,
Ilia
Behavior:
The python tag code is:
import c4d
doc: c4d.documents.BaseDocument
op: c4d.BaseTag
def main() -> None:
polyOp: c4d.BaseObject = op.GetObject()
targetOp: c4d.BaseObject = polyOp.GetDown()
lineUOp: c4d.BaseObject = targetOp.GetNext()
lineVOp: c4d.BaseObject = lineUOp.GetNext()
[A, B, C, D] = polyOp.GetAllPoints()
P = targetOp.GetRelPos()
hl = c4d.modules.hair.HairLibrary()
U, V = hl.GetPolyPointST(P, A, B, C, D, True)
AB, DC, AD, BC = B - A, C - D, D - A, C - B
lineUOp.SetPoint(0, A + AB * U)
lineUOp.SetPoint(1, D + DC * U)
lineVOp.SetPoint(0, A + AD * V)
lineVOp.SetPoint(1, B + BC * V)
In C++ the usage would be very similar:
PolygonObject* polyObjOp; // = static_cast<PolygonObject*>(op);
Vector* ptsPoly = polyObjOp->GetPointR();
Vector A = ptsPoly[0], B = ptsPoly[1], C = ptsPoly[2], D = ptsPoly[3];
Float U = 0, V = 0;
Vector P = pointOp->GetRelPos();
Bool inBoundary = maxon::GeometryUtilsInterface::CalculatePolygonPointST(P, A, B, C, D, true, U, V);
Hi @cybor09,
Thanks for reaching out to us. You can achieve such grouping by simply registering your plugins in a regular way (please find a code snippet below). It's a default behavior that organizes all your plugins under a folder named after your plugin folder.
Let me know if you have any further questions.
Cheers,
Ilia
*.pyp file content:
import c4d, os
from c4d import gui
PLUGIN1_ID = 999121031
PLUGIN2_ID = 999121032
PLUGIN3_ID = 999121033
class PC_12103_1(c4d.plugins.CommandData):
def Execute(self, doc):
print("Execute the 1st command")
return True
class PC_12103_2(c4d.plugins.CommandData):
def Execute(self, doc):
print("Execute the 2nd command")
return True
class PC_12103_3(c4d.plugins.CommandData):
def Execute(self, doc):
print("Execute the 3rd command")
return True
def loadIconBMP(iconName: str) -> c4d.bitmaps.BaseBitmap:
directory, _ = os.path.split(__file__)
fn = os.path.join(directory, "res", iconName)
# Creates a BaseBitmap
bmp = c4d.bitmaps.BaseBitmap()
if bmp is None:
raise MemoryError("Failed to create a BaseBitmap.")
# Init the BaseBitmap with the icon
if bmp.InitWith(fn)[0] != c4d.IMAGERESULT_OK:
raise MemoryError("Failed to initialize the BaseBitmap.")
return bmp
if __name__ == "__main__":
c4d.plugins.RegisterCommandPlugin(PLUGIN1_ID, "1st Cmd", 0, loadIconBMP("icon1.tif"), "", PC_12103_1())
c4d.plugins.RegisterCommandPlugin(PLUGIN2_ID, "2nd Cmd", 0, loadIconBMP("icon2.png"), "", PC_12103_2())
c4d.plugins.RegisterCommandPlugin(PLUGIN3_ID, "3rd Cmd", 0, loadIconBMP("icon3.png"), "", PC_12103_3())
Plugin folder structure:
Hi @chuanzhen,
sorry for the delayed answer.
Thank you for sharing your findings with us! This is a numerical issue in the GetPolyPointST() implementation. I've fixed it but it will only be available in one of our future releases.
Cheers,
Ilia
Hello @君心Jay,
Welcome to the Plugin Café forum and the Cinema 4D development community, it is great to have you with us!
Before creating your next postings, we would recommend making yourself accustomed with our Forum and Support Guidelines, as they line out details about the Maxon SDK Group support procedures. Of special importance are:
First of all there is no "correct" way of doing that. The pattern you should use depend on the context of your goal.
For example, looking at your code snippet it seems that the easiest way for you to make these connections would be to first connect the graph with the outside nodes and then use the MoveToGroup function, which would rewire the connections for you automatically.
This is, however, not the general case. If you would really like to manually wire these ports, you would simply need to find them inside the group and connect them normally using Connect function. The pitfall here is that once you move your sub-graph to the group, it changes its path. This basically means that you'd need to find these nodes using FindNodesByAssetId or GetInnerNodes functions.
Please refer to the draft sketch below that shows both approaches (you need to comment/uncomment corresponding function call in main()).
Cheers,
Ilia
Draft sketch:
import c4d
import maxon
doc: c4d.documents.BaseDocument
mat: c4d.BaseMaterial
nimbusRef: maxon.NimbusBaseInterface
graph: maxon.GraphModelInterface
def main():
global doc, mat, nimbusRef, graph
mat = doc.GetActiveMaterial()
nimbusRef = mat.GetNimbusRef(c4d.GetActiveNodeSpaceId())
graph = nimbusRef.GetGraph()
easy_way()
# manual_wiring()
class rsID:
def StrNodeID(id: str) -> str:
return "com.redshift3d.redshift4c4d.nodes.core." + id
def StrPortID(nodeId: str, portId: str) -> str:
return "com.redshift3d.redshift4c4d.nodes.core." + nodeId + "." + portId
def easy_way():
with graph.BeginTransaction() as transaction:
# The outside value node
valNode: maxon.GraphNode = graph.AddChild(maxon.Id(), maxon.Id("net.maxon.node.type"))
valPortOutput: maxon.GraphNode = valNode.GetOutputs().FindChild("out")
# The inside ABS node
absNode: maxon.GraphNode = graph.AddChild(maxon.Id(), maxon.Id(rsID.StrNodeID("rsmathabs")))
absPortInput: maxon.GraphNode = absNode.GetInputs().FindChild(rsID.StrPortID("rsmathabs", "input"))
absPortOutput: maxon.GraphNode = absNode.GetOutputs().FindChild(rsID.StrPortID("rsmathabs", "out"))
# Existing Standard material node
stdMatNodes: list[maxon.GraphNode] = []
maxon.GraphModelHelper.FindNodesByAssetId(graph, maxon.Id(rsID.StrNodeID("standardmaterial")), True, stdMatNodes)
matNode: maxon.GraphNode = stdMatNodes[0]
matPortOpac: maxon.GraphNode = matNode.GetInputs().FindChild(rsID.StrPortID("standardmaterial", "opacity_color"))
# Connect everything in place
valPortOutput.Connect(absPortInput)
absPortOutput.Connect(matPortOpac)
# Move to group -> rewiring is handled automatically
graph.MoveToGroup(maxon.GraphNode(), maxon.Id("PSRgroupID"), [absNode])
transaction.Commit()
c4d.EventAdd()
def manual_wiring():
with graph.BeginTransaction() as transaction:
# The outside value node
valNode: maxon.GraphNode = graph.AddChild(maxon.Id(), maxon.Id("net.maxon.node.type"))
valPortOutput: maxon.GraphNode = valNode.GetOutputs().FindChild("out")
# The inside ABS node
absNode: maxon.GraphNode = graph.AddChild(maxon.Id(), maxon.Id(rsID.StrNodeID("rsmathabs")))
# Existing Standard material node
stdMatNodes: list[maxon.GraphNode] = []
maxon.GraphModelHelper.FindNodesByAssetId(graph, maxon.Id(rsID.StrNodeID("standardmaterial")), True, stdMatNodes)
matNode: maxon.GraphNode = stdMatNodes[0]
matPortOpac: maxon.GraphNode = matNode.GetInputs().FindChild(rsID.StrPortID("standardmaterial", "opacity_color"))
# Move to group straight away
groupRoot = graph.MoveToGroup(maxon.GraphNode(), maxon.Id("PSRgroupID"), [absNode])
# Create group ports
groupPortInputOutside: maxon.GraphNode = maxon.GraphModelHelper.CreateInputPort(groupRoot, "group_input_id", "grpInput")
groupPortOutputOutside: maxon.GraphNode = maxon.GraphModelHelper.CreateOutputPort(groupRoot, "group_output_id", "grpOutput")
# Connect group to the outside nodes
valPortOutput.Connect(groupPortInputOutside)
groupPortOutputOutside.Connect(matPortOpac)
# Find innder node
innerNodes: list[maxon.GraphNode] = []
maxon.GraphModelHelper.FindNodesByAssetId(graph, maxon.Id(rsID.StrNodeID("rsmathabs")), True, innerNodes)
absNodeInner: maxon.GraphNode = innerNodes[0]
# Find inner node ports
absNodeInnerInput: maxon.GraphNode = absNodeInner.GetInputs().FindChild(rsID.StrPortID("rsmathabs", "input"))
absNodeInnerOutput: maxon.GraphNode = absNodeInner.GetOutputs().FindChild(rsID.StrPortID("rsmathabs", "out"))
# Connect inner node ports to group ports
groupPortInputOutside.Connect(absNodeInnerInput)
absNodeInnerOutput.Connect(groupPortOutputOutside)
transaction.Commit()
c4d.EventAdd()
if __name__ == '__main__':
main()
Hi Tomasz,
There're 3 steps you need to accomplish:
Please find the code sketch that presumable does what you need below.
Cheers,
Ilia
Draft code snippet:
import c4d
doc: c4d.documents.BaseDocument # The currently active document.
ID_SNAP_SCENEHOOK = 440000111
def getModelingSettings() -> c4d.GeListNode:
# Find Snap scene hook
snapHook: c4d.BaseList2D = doc.FindSceneHook(ID_SNAP_SCENEHOOK)
# Search for the modeling settings in its branch info
branchInfo: dict
for branchInfo in snapHook.GetBranchInfo():
if branchInfo.get('name') != 'MdSH':
continue
head: c4d.GeListHead
if head := branchInfo.get('head'):
return head.GetFirst()
return None
def main() -> None:
# Retrieve modeling settings
ModelingSettings: c4d.GeListNode = getModelingSettings()
if not ModelingSettings:
return print('Unexpected error')
# Enable mesh check
ModelingSettings[c4d.MESH_CHECK_ENABLED] = True
# Call select boundary edges button
c4d.CallButton(ModelingSettings, c4d.MESH_CHECK_BOUNDARY_SELECT)
# Run edge to spline command
objects: list[c4d.BaseList2D] = doc.GetActiveObjects(c4d.GETACTIVEOBJECTFLAGS_NONE)
if not c4d.utils.SendModelingCommand(c4d.MCOMMAND_EDGE_TO_SPLINE, objects, c4d.MODELINGCOMMANDMODE_EDGESELECTION):
print('Error on SendModelingCommand() execution')
c4d.EventAdd()
if __name__ == '__main__':
main()
Hi Klaus,
@baca is again completely right! 
Although python has lots of advantages (really fast start for coding, no need in compilation, reloading changes without restarting cinema etc just to mention a couple), however, this doesn't come with no cost. It is quite slow especially in highly loaded parts of code execution (like scene hooks or GetVirtualObjects()).
There's an opportunity to offload expensive parts of your code into C++ library and then call these functions from within your python execution environment. This approach is called Python bindings, you can search more information about it yourself, e.g. here: Python Bindings: Calling C or C++ From Python.
However, this tend to speed things up when you have an expensive task that is executed not too frequently. I'm not aware of what you're doing in your plugin, but it sounds like you have to deal with numerous amount of C4D objects, which drastically slows down your plugin. If that's the case, then I assume the speed up you would gain from the python bindings wouldn't be significant.
Cheers,
Ilia
Hello @gaschka,
Welcome to the Plugin Café forum and the Cinema 4D development community, it is great to have you with us!
Before creating your next postings, we would recommend making yourself accustomed with our Forum and Support Guidelines, as they line out details about the Maxon SDK Group support procedures. Of special importance are:
To set your userdata interface type as a float slider you just need to add c4d.DESC_CUSTOMGUI parameter set to c4d.CUSTOMGUI_REALSLIDER to your userdata container:
squash_and_stretch_container[c4d.DESC_CUSTOMGUI] = c4d.CUSTOMGUI_REALSLIDER
It's also a good idea to specify c4d.DESC_MINSLIDER and c4d.DESC_MAXSLIDER when using sliders.
Cheers,
Ilia
Hi Dan,
The Make Editable command retrieves the cache of your object via GetVirtualObjects() function, which returns just an ordinary BaseObject*. Hence, it is up to plugin to decide what tags should be added to the returned cache object.
In case of Plane By Polygons Generator example there's no such a line of code that creates any tags on the returned cache object, hence none of your tags on this object will survive after Make Editable command.
If you want to keep them, you need to manually copy them over to your returned BaseObject*. This is usually done using CopyTagsTo() function, something that looks like the following:
BaseObject* MyGenerator::GetVirtualObjects(BaseObject* op, const HierarchyHelp* hh)
{
// ... some code
BaseObject* ret = BaseObject::Alloc(Onull); // or likely Opolygon
if (!op->CopyTagsTo(ret, true, NOTOK, false, nullptr))
return BaseObject::Alloc(Onull);
// ... some code
return ret;
}
Note, that here nullptr is used for alias translator for simplicity. Normally, you need to use AliasTrans that would handle tag's dependencies for you.
You can check the GetVirtualObjects() implementation in the Rounded Tube example. Please note, that in this example the CopyTagsTo() function uses false for the 3rd 'variable' argument, which means that variable tags will not be copied over. If you want to make it work with the Vertex Color tag, you need to use either true or NOTOK, depending if you want to copy over all tags or only variable ones.
Cheers,
Ilia
Hello @manudin!
Welcome to the Maxon developers forum and its community, it is great to have you with us!
Before creating your next postings, we would recommend making yourself accustomed with our forum and support procedures. You did not do anything wrong, we point all new users to these rules.
It is strongly recommended to read the first two topics carefully, especially the section Support Procedures: Asking Questions.
These static text separators are just normal separators with provided title. You can do this by assigning BaseContainer instead of boolean (please check the code snippet below).
Cheers,
Ilia
import c4d
from c4d import gui
def EnhanceMainMenu():
menu = c4d.BaseContainer()
menu.InsData(c4d.MENURESOURCE_SUBTITLE, "My Menu 1")
menu.InsData(c4d.MENURESOURCE_COMMAND, "PLUGIN_CMD_{}".format(c4d.Ocube))
menu.InsData(c4d.MENURESOURCE_SEPARATOR, True);
menu.InsData(c4d.MENURESOURCE_COMMAND, "PLUGIN_CMD_{}".format(c4d.Osphere))
m = c4d.BaseContainer()
m.InsData(c4d.MENURESOURCE_SUBTITLE, "My Category")
menu.InsData(c4d.MENURESOURCE_SEPARATOR, m)
menu.InsData(c4d.MENURESOURCE_COMMAND, "PLUGIN_CMD_{}".format(c4d.Oplane))
mainMenu = gui.GetMenuResource("M_EDITOR")
mainMenu.InsData(c4d.MENURESOURCE_STRING, menu)
if c4d.threading.GeIsMainThreadAndNoDrawThread():
c4d.gui.UpdateMenus()
if __name__ == "__main__":
EnhanceMainMenu()
Hi @mikeudin,
Although MemoryFileStruct is a little outdated variant of our in-memory file system, this is the only option to be used in Python API. If using C++ please use RamDiskInterface instead!
MemoryFileStruct is sort of a wrapper over a bytes buffer that the Filename object can point to and hence use it in other parts of our API. This actually means, that similarly to a normal file you can store any data inside and use it as if it was a real file on a disk.
HyperFile class gives you access to some convenient functions for storing different types of data. Normally writing and reading functions of the HyperFile add some meta information to the file or to these chunks of data that you store (one of this extra pieces of info is for example "indent", the identification number that you can use to check that the file you're reading was created by your plugin, or may be by the correct version of your plugin).
In case of Adobe Illustrator file you already have the entire content of the file that you need to put inside the MemoryFileStruct. For that you don't even need HyperFile functions, you just need to convert your string to the bytearray and initialize MemoryFileStruct that points to this bytearray.
The LoadDocument function allows you to use MemoryFileStruct instead of filename, so you just use it in a normal way.
Please check the code snippet below, that shows the described approach.
Cheers,
Ilia
import c4d
AI_CONTENT = """%!PS-Adobe-3.0
%%BoundingBox: 0 0 330 700
%%Pages: 1
%%EndComments
0 setgray
0 setlinecap
1 setlinewidth
0 setlinejoin
10 setmiterlimit
[] 0 setdash
%%EndProlog
%%Page: 1 1
newpath
81 387 m
80 384 80 382 81 381 c
82 379 84 379 88 379 c
151 379 l
154 379 156 379 157 381 c
158 382 158 384 158 387 c
151 635 l
151 637 150 639 149 640 c
148 641 146 642 144 642 c
95 642 l
92 642 90 641 89 640 c
88 639 88 637 88 635 c
81 387 l
177 0 m
171 0 169 2 169 7 c
161 314 l
160 318 157 321 153 321 c
86 321 l
81 321 79 318 79 314 c
70 7 l
70 2 67 0 62 0 c
17 0 l
14 0 12 0 11 2 c
10 3 10 5 10 8 c
27 615 l
27 645 34 666 48 680 c
62 693 84 700 114 700 c
125 700 l
155 700 176 693 190 680 c
204 666 211 645 212 615 c
229 8 l
229 5 228 3 227 2 c
226 0 224 0 222 0 c
177 0 l
closepath
stroke
%%Trailer"""
def main():
contentBytes: bytearray = bytearray(AI_CONTENT.encode(encoding='utf-8'))
mfs = c4d.storage.MemoryFileStruct()
mfs.SetMemoryReadMode(contentBytes, len(contentBytes))
loadedDoc = c4d.documents.LoadDocument(mfs, c4d.SCENEFILTER_OBJECTS | c4d.SCENEFILTER_MATERIALS)
if loadedDoc is None:
raise RuntimeError('Failed to load document!')
c4d.documents.InsertBaseDocument(loadedDoc)
c4d.documents.SetActiveDocument(loadedDoc)
if __name__ == '__main__':
main()
Hi @pyxelrigger ,
Unfortunately your question is out of the scope of support on this forum, namely:
We cannot provide support on learning C++, Python, or one of their popular third-party libraries.
With that's said, I'm kind of missing the main idea behind your question, in other words what are you trying to achieve?
Is it just another (e.g. simply more convenient) data structure for the hierarchy? If so, then you're free to create whatever data structure fits your need the best. For example, check a very fast draft code snippet below.
Is it that you want to track changes of the hierarchy? If so, then you might need to come up with some more complex setup, e.g. involving using the c4d.EVMSG_CHANGE message. Please, refer to a great Ferdinand's answer here: Best way to detect an object has been deleted?
Please also consider visiting our How to ask Questions section of the support procedures for your future postings.
Cheers,
Ilia
A super draft example of nested lists hierarchy representation:
import c4d
doc: c4d.documents.BaseDocument
class HierarchyObject:
def __init__(self, op):
self.op = op
self.children = []
child = self.op.GetDown() if op else doc.GetFirstObject() # recursion entry point
while child:
self.addChild(HierarchyObject(child)) # recursion
child = child.GetNext()
def addChild(self, child):
self.children.append(child)
def toString(self, indentation: int = 0):
indentStr: str = '\t' * indentation
name: str = self.op.GetName() if self.op else '___root___'
s: str = f'{indentStr}<{name}'
if self.children:
s += ':'
for child in self.children:
s += f'\n{child.toString(indentation + 1)}'
s += f'\n{indentStr}'
s += '>'
return s
def __str__(self):
return self.toString()
if __name__=='__main__':
root: HierarchyObject = HierarchyObject(None)
print(root)
Hi @aghiad322,
You can use some dummy element (e.g. empty STATICTEXT) with SCALE_V directive to keep your dropdown aligned to the bottom. Keep in mind that the parent group also needs the SCALE_V. Try Setup #1 (attached below) in your .res file (based on our atom example).
The only downside here would be the gap to the top part when scaled all the way down (notice that on gif).
In case you want to keep your dropdown inside its own group with 2 columns, you can do that as well, but here you again need to make sure all groups use SCALE_V as well. Example Setup #2 is below.
Cheers,
Ilia
Setup #1. Simple example:
CONTAINER Oatom
{
NAME Oatom;
INCLUDE Obase;
GROUP ID_OBJECTPROPERTIES
{
SCALE_V;
REAL ATOMOBJECT_CRAD { ANIM OFF; UNIT METER; MIN 0.01; STEP 0.01; }
REAL ATOMOBJECT_SRAD { UNIT METER; MIN 0.01; STEP 0.01; }
LONG ATOMOBJECT_SUB { MIN 3; MAX 1000; }
BOOL ATOMOBJECT_SINGLE { }
STATICTEXT { SCALE_V; }
LONG ATOMOBJECT_CYCLE
{
ANIM OFF;
CYCLE
{
ATOMOBJECT_CYCLE_1;
ATOMOBJECT_CYCLE_2;
ATOMOBJECT_CYCLE_3;
}
}
}
}
Setup #1. Result
Setup #2. 2-column group example:
CONTAINER Oatom
{
NAME Oatom;
INCLUDE Obase;
GROUP ID_OBJECTPROPERTIES
{
SCALE_V;
REAL ATOMOBJECT_CRAD { ANIM OFF; UNIT METER; MIN 0.01; STEP 0.01; }
REAL ATOMOBJECT_SRAD { UNIT METER; MIN 0.01; STEP 0.01; }
LONG ATOMOBJECT_SUB { MIN 3; MAX 1000; }
BOOL ATOMOBJECT_SINGLE { }
GROUP
{
SCALE_V;
COLUMNS 2;
STATICTEXT { SCALE_V; }
STATICTEXT { JOINEND; }
LONG ATOMOBJECT_CYCLE
{
ANIM OFF;
CYCLE
{
ATOMOBJECT_CYCLE_1;
ATOMOBJECT_CYCLE_2;
ATOMOBJECT_CYCLE_3;
}
}
STATICTEXT { JOINEND; }
}
}
}
Setup #2. Result:
Hi @blkmsk ,
Thank you for sharing your experience and reporting the issue. I've created a ticket in our internal bug tracking system.
Cheers,
Ilia
Hello @pchg,
Welcome to the Plugin Café forum and the Cinema 4D development community, it is great to have you with us!
Before creating your next postings, we would recommend making yourself accustomed with our Forum and Support Guidelines, as they line out details about the Maxon SDK Group support procedures. Of special importance are:
Unfortunately, your question is lacking precise information on the context of your problem. The issue of C4D not being able to find a plugin can be originating from multiple reasons, including issues on the third party library side, which we cannot provide any support for.
In case we have misunderstood your question, I would kindly ask you to elaborate on the context of the problem.
Thanks for your understanding,
Ilia
Hi @yaya,
As this forum is mainly for the development related topics and your question is heavily in the end user area, I suggest you to reach out to our Support Center regarding your Cinema 4D worlflow related questions.
In case I misunderstood your question and it is effectively development related, please elaborate on the context of your question and provide a code snippet that highlights the issue you're trying to solve as per our Support Procedures.
Cheers,
Ilia
Hi Dan,
There's something fishy going on with volume builder when using undo stack. There's no rocket science in the input list of the volume builder, namely it just contains a tree of BaseLinks, so whatever changes are performed in the original object should be reflected by the input list. However, executing undo operation is a little special in a way that it changes pointer to the baseobject (you can easily see that in the Active Object Dialog tool: when moving object, it's pointer is the same, however, when performing undo operation, it's address is changed and hence marked in red):
It sounds to me like a bug in the build volume, namely improper undo event handling. I've created a bug report (ITEM#529307) in our internal bug tracking system.
I think the best workaround for you is to use hierarchy access function GetDown() instead of GetInputObject().
Cheers,
Ilia