Calculate Rigid Transform Matrix to match two identical objects
-
Hey there!
For the following scenario: I have two identical objects obj1 and obj2. I can get these matrices for the objects with built-in functions getMg and SetMg. However, even if I obj2.setMg(obj1.getMg), they may still not overlap since the anchor point may be located differently relative to the points themselves (which I can get using obj.getAllPoints). How would I create a Matrix m to obj2.setMg(m) such that the objects overlap?
I know that I need to created a rigid / euler transform matrix since no scaling or shearing is needed, however it seems that all solutions for that require solving a linear linear matrix equation; which is often done using numpy which we don't have in c4d.
So: Am I maybe overlooking something that's already in the SDK, or do I need to reimplement the equation solving in plain python to calculate the rigid transform?
Any help appreciated!
- Jerome
-
Hello @HerzogVonWiesel,
Thank you for reaching out to us. I am struggling a bit with understanding what you want to be done here. Math terminology is notoriously context dependent, so let me clear up a few things first.
I have never heard the term "rigid-matrix" before. Do you mean a rigid transform? With the
Matrixtype, all transforms are rigid, i.e., linear, i.e., happen in Euclidean space. The type also does not support projections (a.k.a. homogeneous coordinates). But I do not see how all this relates to your problem. I am also unsure what you mean by 'anchor point', I assume you are talking about the mean point of all points in a point object? So, not the origin as defined by the transform of the object, but the origin in local space of all vertices defined as their mean value?In general, it sounds a bit like that you want to do what often has been discussed under the label "move the axis of an object" in this forum. Since then, we have created the Geometry examples. I would recommend having a look at these two examples in particluar:
- operation_transfer_axis_s26.py: Demonstrates how to 'transfer' the axis of a point object to another object while keeping its vertices in place.
- operation_flatten_polygons_s26.py: Demonstrates how to deform points of a point object at the example of 'flattening' the selected polygons in a polygon object.
The first example should be pretty close to what you want to do. The second example might be relevant because in the context of calculating the mean of vertices and normals.
What is missing is the implied task of your question that you want to 'match' two objects. I.e., you have two point clouds P and Q and ask "what is the transform T that transforms P into Q?". The answer to this can be very hard, depending on the degree of similarity of P and Q. But when we can for example expect their first polygon always to be in a pair relation, then you can just construct a frame for each normal of these polygons and the delta between the two frames is then your transform T. When you do not want to fix just orientation, then you would also have to include the delta between the center points of these two polygons to create a full transform and not just a frame.
Cheers,
Ferdinand -
Thank you so much for the response @ferdinand !
I'll attach 2 pictures to show what I'm talking about.
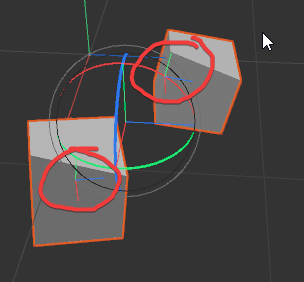
It is the same object, but the anchor point is somewhere else compared to the points of the geo (on top of being somewhere else globally); so when I create an instance of the second object with a reference to the first object and set the global Matrix transform to the matrix transform of the object I replaced by an instance, I get the following (instead of the instance overlaying perfectly):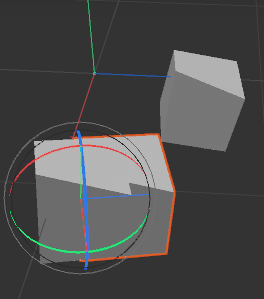
As you said, I could pick a polygon for both objects (since I assume the topology to be the same, even if the points and object could be positioned / rotated differently) and try to derive the needed transform that way; though then I'm a little lost as to how to calculate it and apply it (to the points or the instance? First on the points, then the inverse on the instance object? I'm not sure as you can see).
EDIT: Alright, so we probably want obj1_instance.SetMg(obj2.GetMg()), and then apply DeltaMg to the points of obj1_instance, where DeltaMg = difference between polygon1_obj1 and obj1.GetMg() + difference between polygon1_obj2 and obj2.GetMg() (or something like that, just trying to make sense here)Thing is, I'm also unsure of what the C4D SDK already has implemented that we could use for this problem, and I don't think we need to manually get up with every function in plain python.
Thanks again for your help already ferdinand!
-
Hey @HerzogVonWiesel,
when the axis of your two objects is identical, you won't get anywhere with
BaseObject.GetMg()because that is that axis. The matrix/transform of an object in global space is (mg stands for matrix global) is just the coordinate system in which the points and child objects of an object operate.Or in other words, when you have to go into point mode, select all points, and move, rotate, and scale them to match object Q onto object P, then you have to also manipulate the points in code.
Get/SetMg/Mlare the equivalent of moving, rotating, and scaling an object in object mode. The global matrix of an object IS quite literally its axis you see in the editor. So, when you have selected all points of object Q and randomly transformed them, you must find that transform. For that you need to establish a frame of reference for each object so that you can compute that transform delta between them. FInding these frames can be insanely hard when the objects do not share a topology; but they seem to do in your case.When that is the case, an easy way to compute a frame (a.k.a., the orientation part of a transform, sometimes also called basis) is to construct one on a polygon with the same index of each object. In the Matrix Manual I showed once how to construct a transform from a vector and an up-vector. Here you would not even need an up-vector since a polygon defines all three degrees of freedom. For a triangle with the points a, b, and c and the edges e1, e2, and e3, you can construct a frame on point a with the edges e3 and e1 (see example in the manual for details). When you also want to compute the offset and not only orientation delta, you would have to define the point a as the offset of that constructed transform.
The delta of two transforms is computed with multiplication and the inversion operator. The inverse of a transform is its opposite operation. When you have a transform T which rotates by 90° on the x-axis and translate by -10 units on the y axis, then its inverse ~T would rotate by -90° on x and translate by 10 on y. Or in other words
T * ~T = 0. When we now have two non-identical transforms, we can compute in this manner their delta. For the transforms S and T,M = S * ~Twould for example be the transform that transforms from S to T; i.e.,S * M = T.When you have your delta, you just have to apply it to each point in the object you want to transform in this manner.
 I would recommend having a look at the geometry code examples I linked to above and the Matrix manual, as I went there already over a good deal of the basics. When you are then still stuck please share your existing code and we will help you [1].
I would recommend having a look at the geometry code examples I linked to above and the Matrix manual, as I went there already over a good deal of the basics. When you are then still stuck please share your existing code and we will help you [1].Cheers,
Ferdinand[1] With the exception of higher level topics such as similarity metrics, i.e., the case that two objects look similar, but do not share a topology.
-
Thanks @ferdinand !
That really cleared up a lot for me. I think I now know how to apply the transforms and in which order, though it seems the missing piece seems to be how to construct the matrix from the object's polygon: I didn't quite understand your process, what do you mean by frame? I'm thinking of the "classic" way of taking two edges of the polygon, calculating an orthogonal vector of those and then we have our new base vectors of the matrix (and then concatenate that with the transform to point a); Yeah, I don't think that's the best way to do it, so I'd love to get clarification on that!
- Jerome
-
Hello @HerzogVonWiesel,
The term frame (of reference) is just another word for the basis of a coordinate system, i.e., the three basis vectors that make up a coordinate system. The basis part of a
c4d.Matrixis shown in blue in the image below: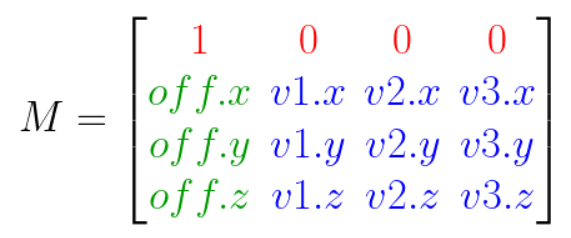
It has been taken from the Matrix Manual I have mentioned. And yes, a frame is usually constructed with the help of the cross product to ensure the orthogonality of the frame (although that is technically not required as the
Matrixtype can also define non-orthogonal matrices). The manual also contains that code example for constructing aMatrix(i.e., also a frame) I mentioned. I would also recommend having a look at theoperation_transfer_axis_s26.pyexample I linked to above, as this contains another part of what is here relevant for you: Computing the delta between two trasnforms.Cheers,
Ferdinand -
Hi @ferdinand !
I've looked through the examples and used them as a base, as well as consulted the Manual a few times, so I'm sharing my current, not working solution:
def ConstructMatrixFromPolygon(polygon: c4d.CPolygon, object: c4d.PointObject) -> c4d.Matrix: # get the points of the polygon a = object.GetPoint(polygon.a) b = object.GetPoint(polygon.b) c = object.GetPoint(polygon.c) e1 = b - a e2 = c - a z = e1.GetNormalized() temp = e2.Cross(z) y = z.Cross(temp).GetNormalized() x = y.Cross(z).GetNormalized() return c4d.Matrix(off=a, v1=x, v2=y, v3=z) def TransferAxisTo(node: c4d.PointObject, target: c4d.PointObject) -> None: """Transforms the points of #node such that they are the same w.r.t. their coordinate system as the points in target are w.r.t. their coordinate system while keeping its coordinate system in place. Args: node target """ if not isinstance(node, c4d.PointObject): raise TypeError(f"Expected {c4d.PointObject} for {node}.") # Get the global matrix of #node and #target which are the absolute transforms, i.e., absolute # coordinate systems which govern these two objects. mgNode = node.GetMg() mgTarget = target.GetMg() # Get the document of #node. nodeDoc = node.GetDocument() if nodeDoc is None: raise RuntimeError(f"'{node.GetName()}' is not attached to a document.") # Open an undo stack for the changes and add an undo item for the point and matrix changes. if not nodeDoc.StartUndo(): raise RuntimeError("Could not open undo stack.") if not nodeDoc.AddUndo(c4d.UNDOTYPE_CHANGE, node): raise RuntimeError("Could not add undo item.") polygonNode = node.GetPolygon(0) polygonTarget = target.GetPolygon(0) m1 = ConstructMatrixFromPolygon(polygonNode, node) m2 = ConstructMatrixFromPolygon(polygonTarget, target) mgDeltaTarget = ~mgTarget * m2 mgDeltaNode = ~mgNode * m1 mgDelta = mgDeltaNode * ~mgDeltaTarget node.SetAllPoints([p * mgDelta for p in node.GetAllPoints()]) node.Message(c4d.MSG_UPDATE) returnI tried to do it as you described in your post, with the example code as a base: I sketched the transforms on paper to visualize them for myself; that's how I came up with the mgDelta and mgDeltaXs.
Still, as I said, it's not really working; so if you see any glaring issues I'd love to hear them!
Cheers, Jerome
PS: Did I understand correctly that Matrix Multiplication is left-bound in C4D? Such that X * Y * Z = Z(Y(X)) ?
-
Hey @HerzogVonWiesel,
At quick glance this all looks correct, good job! Will have a look on Monday what is going wrong there for you.
edit: You are at least missing a
BaseDocument::EndUndobut that should not be the cause of your problems. At a second glance,mgDeltaTarget = ~mgTarget * m2 mgDeltaNode = ~mgNode * m1 mgDelta = mgDeltaNode * ~mgDeltaTargetthis section also does not look quite right. All points are already in local coordinates, so when you try to undo the global transform of their host, e.g.,
~mgTarget * m2, you screw things up (unlessmgTragetandmgNodeare the same transform). It should be more something like thism1 = ConstructMatrixFromPolygon(polygonNode, node) m2 = ConstructMatrixFromPolygon(polygonTarget, target) mgDelta = m2* ~m1 node_m1.SetAllPoints([p * mgDelta for p in node_m1.GetAllPoints()])To for example align all points in m1 with m2. You might have to switch around
mgDelta = m2* ~m1tomgDelta = ~m1 * m2as the two operations are not the same and it can be tricky figure out in your head which the correct rotation order is. But that is all a guess, will have closer look on Monday.Cheers,
Ferdinand -
Hello @HerzogVonWiesel,
So, I was right, you got computing the delta a bit backwards and
mgDeltashould be justm2 * ~m1. I also fixed some other minor stuff.PS: Please post executable code in the future. Here I had first to write a
__main__guard to gather the inputs myself, add imports, etc. Not that much work in this cave but still avoidable work.Cheers,
FerdinandFile: align_local_frames.c4d
Result:
local-player
Code:"""Aligns the local frame of an object named #source to the local frame of an object #target. The local frame established over the first polygon of both objects. """ import c4d doc: c4d.documents.BaseDocument # The active document. def ConstructMatrixFromPolygon(obj: c4d.PolygonObject, index: int) -> c4d.Matrix: """ Note (Ferdinand): This is all correct, it is however a bit odd to make #e1 the z axis. Usually, one would want the z-axis (i.e., v3, the k component of the basis) to be the vertex normal of the vertex #a, i.e., what you declared as #y. But doesn't really matter in this case. You should also be careful with the symbols you use, your variable #object did shadow the central Python type of the same name. """ polygon: c4d.CPolygon = obj.GetPolygon(index) a = obj.GetPoint(polygon.a) b = obj.GetPoint(polygon.b) c = obj.GetPoint(polygon.c) e1 = b - a e2 = c - a z = e1.GetNormalized() temp = e2.Cross(z) y = z.Cross(temp).GetNormalized() x = y.Cross(z).GetNormalized() return c4d.Matrix(off=a, v1=x, v2=y, v3=z) def AlignLocalFrames(source: c4d.PointObject, target: c4d.PointObject, alignGlobalTransform: bool = True) -> None: """Transforms the points of #source in such manner that its points are in the same frame of reference as #target. The frame of reference is established over the first polygon of both objects; this function assumes them to be in an undistorted pair relation. Also aligns the global transform of #source to #target when #alignGlobalTransform is #True. """ if not isinstance(source, c4d.PointObject): raise TypeError(f"Expected {c4d.PointObject} for {source}.") nodeDoc = source.GetDocument() if nodeDoc is None: raise RuntimeError(f"'{source.GetName()}' is not attached to a document.") if not nodeDoc.StartUndo(): raise RuntimeError("Could not open undo stack.") if not nodeDoc.AddUndo(c4d.UNDOTYPE_CHANGE, source): raise RuntimeError("Could not add undo item.") if alignGlobalTransform: source.SetMg(target.GetMg()) # Construct a frame of reference on both objects, including the translation component. m1: c4d.Matrix = ConstructMatrixFromPolygon(source, 0) m2: c4d.Matrix = ConstructMatrixFromPolygon(target, 0) # Compute the delta between m1 and m2, i.e., the transform that is necessary to transform m1 # into m2. mgDelta: c4d.Matrix = m2 * ~m1 # Transform all points in m1 onto m2 (according to our delta) and update Cinema 4D. source.SetAllPoints([p * mgDelta for p in source.GetAllPoints()]) source.Message(c4d.MSG_UPDATE) nodeDoc.EndUndo() c4d.EventAdd() return if __name__ == "__main__": # Attempt to run #AlignLocalFrames on a #source and #target object. source = doc.SearchObject("source") target = doc.SearchObject("target") if None in (source, target): raise RuntimeError() AlignLocalFrames(source, target, alignGlobalTransform=True) -
@ferdinand you are amazing!
Thank you so much for your help, this is it. Now only remains the last step until my script to automatically recognize and replace duplicate objects with instances is complete: The UI. But that should be a quick one.Thank you so much for your help again Ferdinand, you are a saint. Have a superb week and best wishes from Potsdam!
- Jerome