pythonsdk doc Matrix manunl error?

[chuanzhen]

Hi,
When I read the matrix manual in python sdk doc, I found that the descriptions of 1 and 2 seem contradictory. In c4d, counter-clockwise rotation (ccw) displays a positive value 90 °, while clockwise rotation (cw) displays a negative value -90 °. However, in image marker 2, the transformation should be clockwise cw 90 ° (i.e. R.B=-90 °), not ccw90 °

[ferdinand]

Hey @chuanzhen,

Thank you for reaching out to us. I am not quite sure that I can follow. The manual for sure could be improved, as I probably wrote this more technically than it has to be, but I would say the text and image are correct.

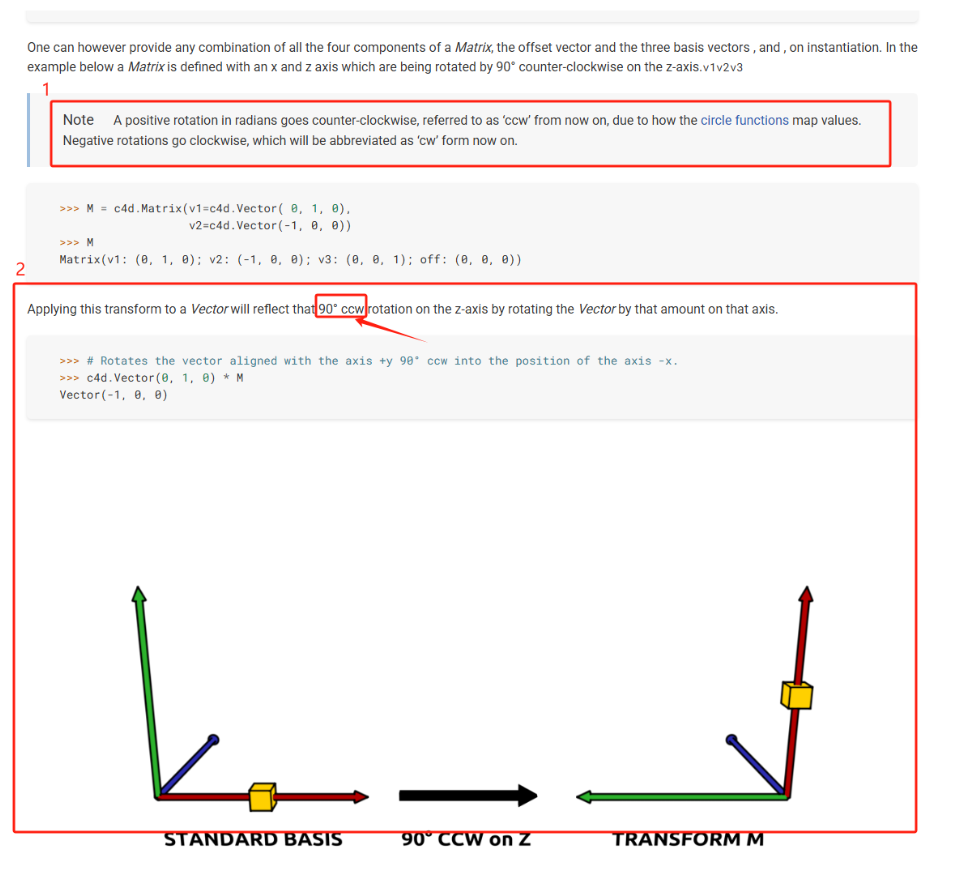
As the manual states, the transform constructed there, is a 90° CCW rotation around the z axis. Which is also what I tried to illustrate below. What is illustrated there, is also more the idea that transforms do not rotate points but rather the coordinate systems in which a point lives.

I do not see anywhere any negative values printed. That would also contradict a bit the cw and ccw notation as they replace +/-. When we talk about cw/ccw, we have to imagine a plane spanned by the axis perpendicular to the rotation axis, e.g., the XY plane for the z axis in the image below. And imagine there a clock. CCW means then the direction I have marked with the blue arrow below. And when you look at the axis gizmo on the right, you can see it exactly being rotated into that direction.

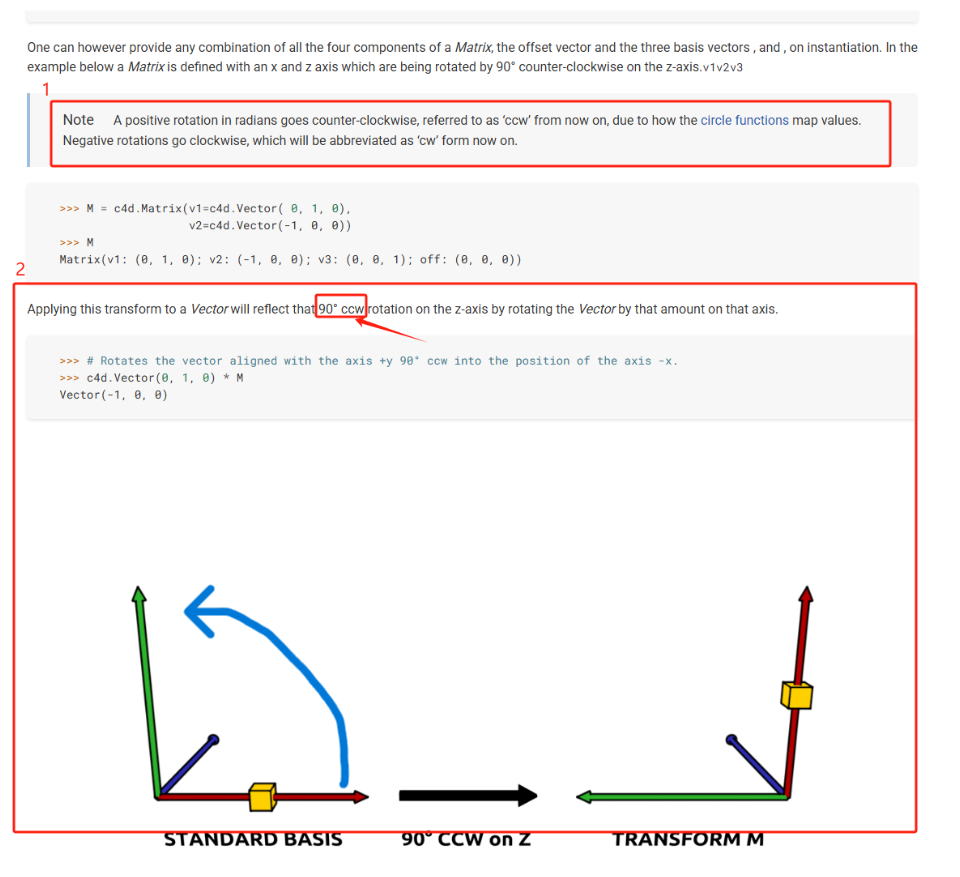
The other thing which might lead to confusion here, is that humans tend to associate positive numbers with a clockwise motion. But that is exactly the point of that note. The circle functions do the opposite of what humans consider natural. The 2D rotation matrix M(theta) will make a 2D point rotate counter clockwise on the unit circle when you add positiv values to theta and clockwise when you add negative values.

Cheers,
Ferdinand

[chuanzhen]

@ferdinand Thank you for explanation. The point of confusion should be marked as 2 in the image. in doc the counterclockwise rotation (ccw) refers to the counterclockwise rotation from the spatial perspective of the image. but for the same rotation, the z-axis should have rotated clockwise（cw）. However, in any case, the calculation is correct, only the description is different。
(Describing a rotation of an axis, it is assumed that a person looks in the negative direction from the positive direction of the axis, and based on this, counterclockwise and clockwise are defined)