Blend matrices
-
Hi everyone,
Is there any python util to linearly interpolate between two transformation matrices by parameter, similar to c4d.utils.MixVec?
For now I see the only way to decompose matrices, blend and compose blended matrix from the blended values... -
Hi baca, thanks for reaching out us.
With regard to your question, I'm not aware of any explicit operator that linearly interpolates matrixes, but considering that a matrix can be easily multiplied by a scalar, getting linear interpolation for matrix is
c = ((1 - x) * a + x * b )as much as for scalars or vectors.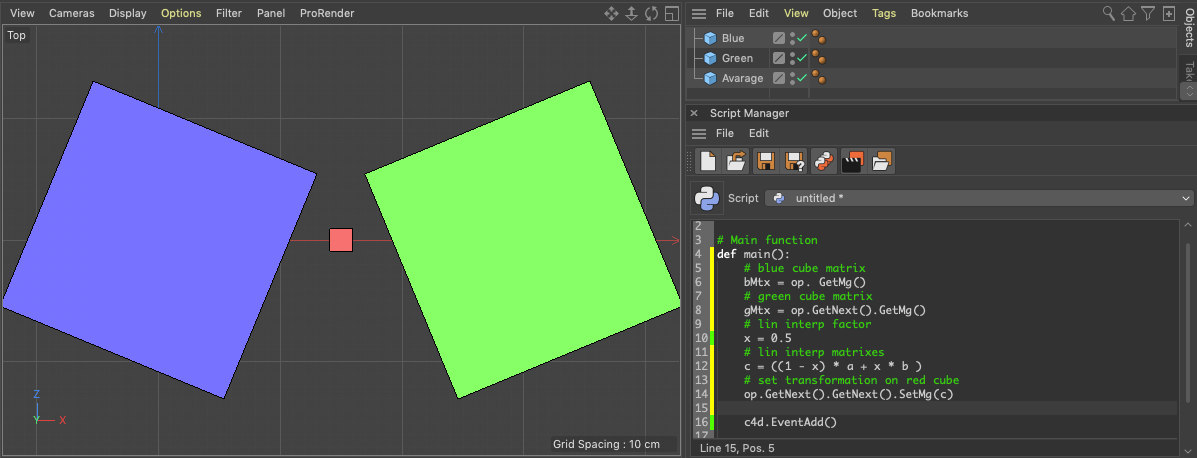
Cheers, R
-
@r_gigante said in Blend matrices:
((1 - x) * a + x * b )
Thanks for your help @r_gigante.
Actually your formula produce some results. But it's not accurate, except specific cases.Due to transformation matrix nature, Scale and Rotation sharing same sub-matrix values.
Also Rotation express itself with trigonometric values.
Straight linear interpolation not suit for matrix blending, it cause scale and/or rotation distortion.I'll dive into self-made interpolation method.
-
If anyone interested:
def MatrixBlend(mxA, mxB, t): quatA = c4d.Quaternion() quatA.SetMatrix(mxA) quatB = c4d.Quaternion() quatB.SetMatrix(mxB) return utils.MatrixMove( utils.MixVec(mxA.off, mxB.off, t) ) * utils.QSlerp(quatA, quatB, t).GetMatrix() * utils.MatrixScale( utils.MixVec(mxA.GetScale(), mxB.GetScale(), t) ) -
Thanks a lot Baca and I apologize for the hurried and shallow answer.
Looking deeper in the argument the Computer Animation: Algorithms and Techniques reports: "While it should be obvious that interpolating the translation is straigthforward, it is not at all clear how to go about interpolating the rotations. In fact, it is the objective of this discussion to show that interpolation of orientations can be a problem. A property of 3x3 rotation matrix is that the rows and columns are orthonormal. Simple linear interporlation between the nine pairs of numbers that make up the two 3x3 rotation matrices to be interpolated will not produce intermediate 3x3 matrices that are orthonormal and are, therefore, not rigid body rotations. It should be easy to see that interpolating from a rotation of +90 deg about the y-axis to a rotation of -90 degrees about the y-axis results in an intermediate transformation that is nonsense.
So direct interpolation of transformation matrices is not acceptable. There are alternatives representation that are more useful than transformation matrices in performing such interpolations: fixed angle, Euler angle, axis angle, quaternions."Considering your answer providing a reasonable solution using quaternions, I've played something similar using fixed angle
def MatrixBlendFixedAngle(mxA, mxB, t): # get mxA scale AScale = mxA.GetScale() # get mxA offset AOff = mxA.off # remove from mxA the scale to retrieve rotation mxA.Scale(c4d.Vector(1/AScale.x, 1/AScale.y, 1/AScale.z) ) # retrieve the HPB representation of mxA AHPB = utils.MatrixToHPB(mxA) # get mxB scale BScale = mxB.GetScale() # get mxB offset BOff = mxB.off # remove from mxB the scale to retrieve rotation mxB.Scale(c4d.Vector(1/BScale.x, 1/BScale.y, 1/BScale.z) ) # retrieve the HPB representation of mxB BHPB = utils.MatrixToHPB(mxB) # execute the linear interpolations for offset, scale and HPB COff = (1 - t) * AOff + t * BOff CScale = (1 - t) * AScale + t * BScale CHPB = (1 - t) * AHPB + t * BHPB # calculate mxC from interpolated HPB mxC = utils.HPBToMatrix(CHPB) # add the interpolated scale mxC.Scale(CScale) # add the interpolated offset mxC.off = COff return mxCFinally with regard to your quaternion solution, for those who are interested in, a discussion on how to make use of quaternions is on GameDev.
Cheers, R
-
This post is deleted!