How can I add an offset to the global matrix of an object that is rotated?

[HerrMay]

Hi guys,

as the title already suggests I wonder how I can add an arbitrary offset value to the global matrix of an object that is rotated. In that way that the object moves along that angled position plus the given offset?

I tried adding the offset to the z axis of the 'off' component of the objects global matrix. But without any luck. The object is then of course moving along the world axis by the amount of the offset.

I hope someone can help me here with these dreadful matrices.

Cheers,
Sebastian

[ferdinand]

Hello @HerrMay,

Thank you for reaching out to us. Yeah, transforms can be a tricky subject, I would recommend having a look at the Matrix Manual as it does explain some fundamentals.

Your question was quite clear, but there is always some ambiguity with transform questions unless one uses a super mathematical language. But I think I got what you meant and have provided an example below.

Cheers,
Ferdinand

Result:

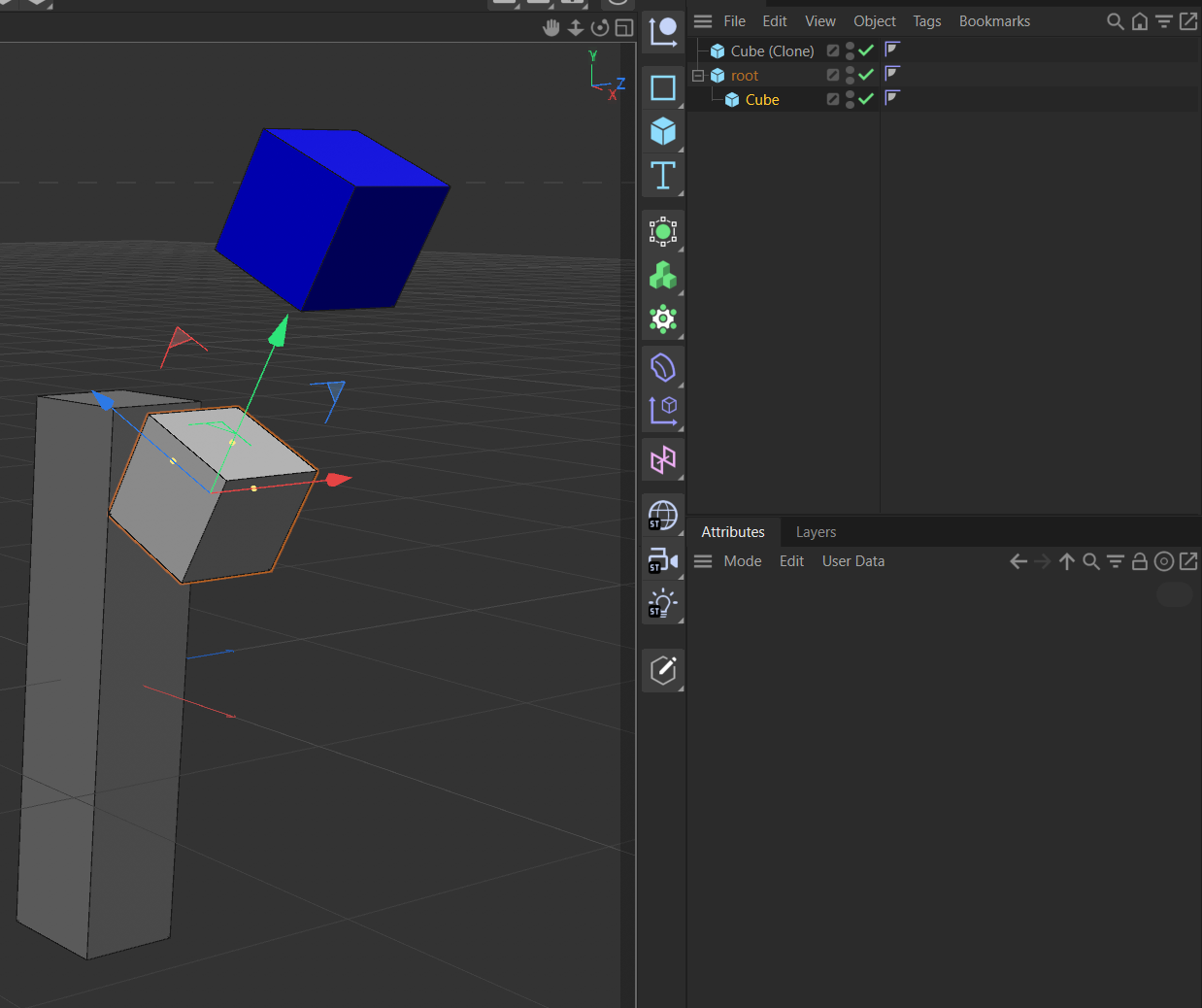
The input object is selected, in blue an object translated by (0, 500, 0) units in the local coordinate system of the selected object.

Code:

"""Demonstrates translating an object in its own local coordinate system.

Must be run as a Script Manager script with an object selected.

Related:
    https://developers.maxon.net/docs/py/2023_2/manuals/data_algorithms/classic_api/matrix.html
"""

import c4d
import typing

doc: c4d.documents.BaseDocument  # The active document
op: typing.Optional[c4d.BaseObject]  # The active object, None if unselected

def main() -> None:
    """
    """
    if not op:
        raise RuntimeError("Please select an object.")

    # Clone the selected object and insert the clone into the document, so that we have this out of 
    # the way.
    clone: c4d.BaseObject = op.GetClone(c4d.COPYFLAGS_NO_HIERARCHY)
    if not clone:
        raise MemoryError("Could not clone object.")

    clone.SetName(f"{op.GetName()} (Clone)")
    clone[c4d.ID_BASEOBJECT_USECOLOR] = c4d.ID_BASEOBJECT_USECOLOR_ALWAYS
    clone[c4d.ID_BASEOBJECT_COLOR] = c4d.Vector(0, 0, 1)
    doc.InsertObject(clone)

    # The vector with which we want to translate something.
    p: c4d.Vector = c4d.Vector(0, 500, 0)

    # Translate an object inside its own local coordinate system.
    #
    # Doing this means simply multiplying our translation vector #p with the global matrix of the 
    # object and setting the result as the new offset of the global matrix. Remember, multiplying a 
    # point #p with the matrix #M will yield a global point #q that is in the same relation to #M as
    # #p is to the global frame. I.e., in this case it will yield a vector #q that is in the same 
    # relation with #mg as the vector (0, 500, 0) is with the world frame.
    mg: c4d.Matrix = op.GetMg()
    mg.off = mg * p
    clone.SetMg(mg)

    c4d.EventAdd()

if __name__ == '__main__':
    main()

[HerrMay]

Hello @ferdinand,

sorry for being a bit nebulous. I wasn't sure how I should explain what I mean in a way that would illustrate it a bit better.

Actually I hab a look at the matrix manual. But as someone who had no matrix calculation lessons in school, it's a bit overwhelming at first glance.

Yes, you guessed correctly. That is exactly what I wanted. Thank you once again.

Is the multiplication of a matrix with a vector (mg.off = mg * p) essentially the same what mg * c4d.utils.MatrixMove(vec) does?

Cheers,
Sebastian

[ferdinand]

Hello @HerrMay,

Is the multiplication of a matrix with a vector (mg.off = mg * p) essentially the same what mg * c4d.utils.MatrixMove(vec) does?

No, mg * p multiplies a matrix by a vector which will yield the transformed vector p'. mg * c4d.utils.MatrixMove(vec) on the other hand multiplies two matrices, yielding the combined transform of them, a new matrix.

What would be equivalent to mg * p is mg * c4d.utils.MatrixMove(p) * c4d.Vetcor(0, 0, 0). Please note that the whole subject is also out of scope of support as declared in the forum guidelines. I understand that the subject is a common barrier for the more on the artist-sided leaning users of ours, and I help where I can, but we cannot teach you vector math, linear algebra, or however you want to label this subject.

Find below a short code example.

Cheers,
Ferdinand

Output:

M = Matrix(v1: (1, 0, 0); 
           v2: (0, 1, 0); 
           v3: (0, 0, 1); 
           off: (0, 100, 0))
p = Vector(100, 0, 0)

M * p = Vector(100, 100, 0)
M * c4d.utils.MatrixMove(c4d.Vector(100, 0, 0)) = Matrix(v1: (1, 0, 0); 
                                                         v2: (0, 1, 0); 
                                                         v3: (0, 0, 1); 
                                                         off: (100, 100, 0))
M * c4d.Vector(100, 0, 0) = Vector(100, 100, 0)
N * c4d.Vector(  0, 0, 0) = Vector(100, 100, 0)
M * c4d.utils.MatrixMove(p) * c4d.Vector(0, 0, 0) = Vector(100, 100, 0)

Code:

import c4d

# Let us assume #M to be the global matrix/transform of some object #op. View it as a tool to 
# transform a point in global space into the local coordinate system of #op.
M: c4d.Matrix = c4d.Matrix(off=c4d.Vector(0, 100, 0))

# The matrix #M now has this form:
#
#   | v1     1    0    0 |   # The "x-axis" of the coordinate system defined by #M.
#   | v2     0    1    0 |   # The "y-axis" of the coordinate system defined by #M.
#   | v3     0    0    1 |   # The "z-axis" of the coordinate system defined by #M.
#   ---------------------- 
#   | off    0  100    0 |   # The origin of the coordinate system defined by #M.
#
# I.e., #M has the standard orientation and scale and only translates all things by 100 units
# on the y-axis. So, the object #op would have the Euler angles (0°, 0°, 0°), the scale (1, 1, 1) 
# and the position (0, 100, 0) in world coordinates.

# Define a vector #p to transform and print both #M and #p.
p: c4d.Vector = c4d.Vector(100, 0, 0)
print(f"{M = }")
print(f"{p = }")

# Transforming a point #p by a matrix #M will yield a point #q that is in the same relation to #M
# as #p is to the global frame.
q: c4d.Vector = M * p

# #q will be the vector (100, 100, 0) because , (100, 100, 0) and #M are the same relation as #p
# and the identity matrix are, a.k.a., the world frame. In a less technical way, (0, 100, 0) is the
# origin of the coordinate system defined by #M. And to express #p in a manner as if #M would be
# its coordinate system, we have to add (0, 100, 0), because that is the new origin. For orientation
# and scale it works more or less the same, I would recommend having a look at the Matrix manual or
# Wikipedia article on the subject.
print (f"{M * p = }")

# We can construct new transforms in many ways (again, Matrix Manual :)), one of them is by 
# combining multiple transforms via matrix multiplication.

# We "add" the translation transform (100, 0, 0) to #M. Note that matrix multiplication is not 
# commutative, i.e., "M * N = N * M" does not always hold true. In this case it would because only
# translations are involved.
N: c4d.Matrix = M * c4d.utils.MatrixMove(c4d.Vector(100, 0, 0))
print(f"{M * c4d.utils.MatrixMove(c4d.Vector(100, 0, 0)) = }")

# To get the same point as #q when multiplying a point #r with #N, we must pick the null-vector
# because the origin of #N is already at where M * (100, 0, 0) is.
print (f"{M * c4d.Vector(100, 0, 0) = }")
print (f"{N * c4d.Vector(  0, 0, 0) = }")

# We can also do it in one operation:
print (f"{M * c4d.utils.MatrixMove(p) * c4d.Vector(0, 0, 0) = }")