3D -> 2D and back with perspective
-
Hello coders,
since this is a question about algorithms I figured I'd post this here. Also this is mostly me hoping that someone will drop some wisdom on me in terms of 3D programming.
Problem
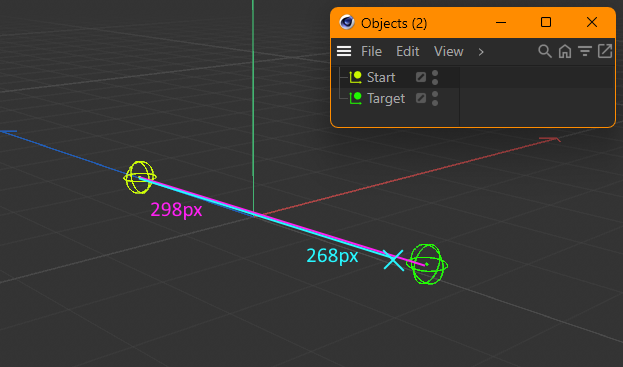
So I got two different positions in 3D space,
StartandTarget. When I look at them in the C4D viewport I need to calculate a new point which is between the two points, but 30 pixels before the target.Take a look at this example where the distance in pixels on the screen is 298, so I need a new point which is 268 pixels away from
Start(298px - 30px), blue X marks the desired spot.
However this point must exist in world space.So my thought process was this:
- Get screen coordinates of both points using
BaseView.WS. - Calculate how far away the new point is from
Startin percent relative to the screen distance toTarget. - Create a new point in screen space using this calculated ratio by doing
Start + Direction * Distance * Ratio. - Transform to world coordinates using
BaseView.SW.
The new point will be in the correct screen coordinates, so x and y are fine. However z is messed up which I can only assume is because of the camera perspective.
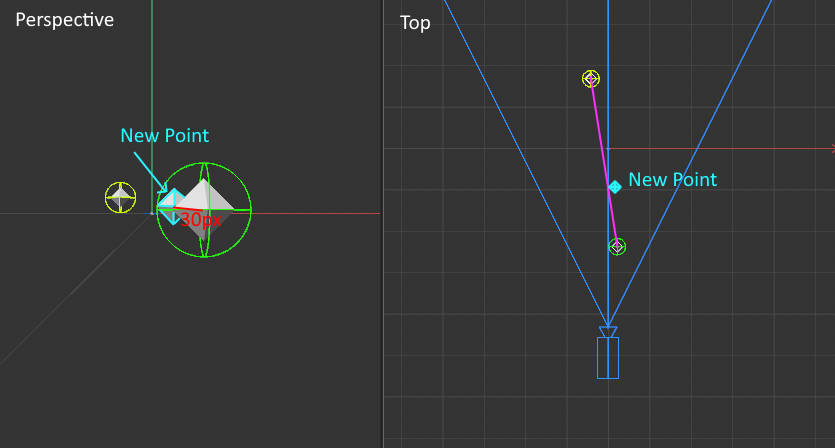
Note in the following demo how both the target and the new point are always the same distance apart from each other in Perspective View while the z coordinate in Top View prevents the point from being on the desired pink line between the two points:
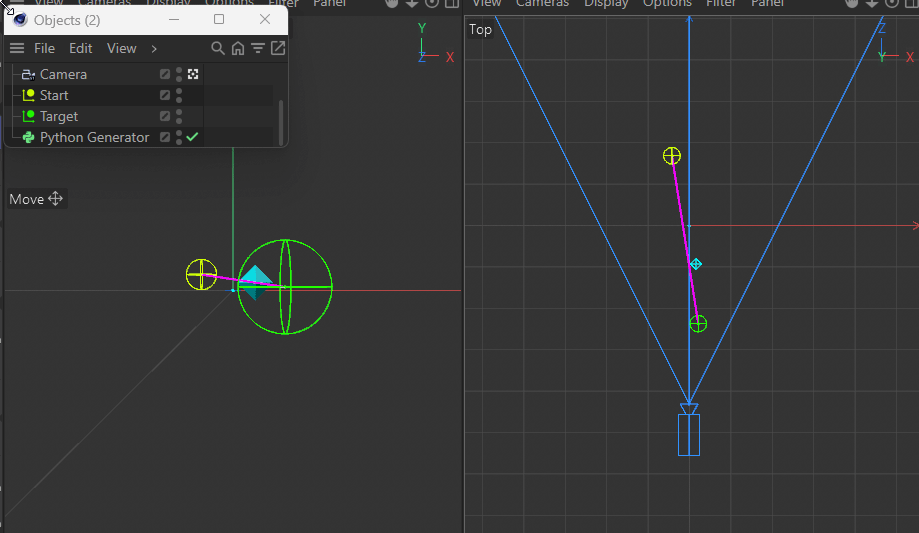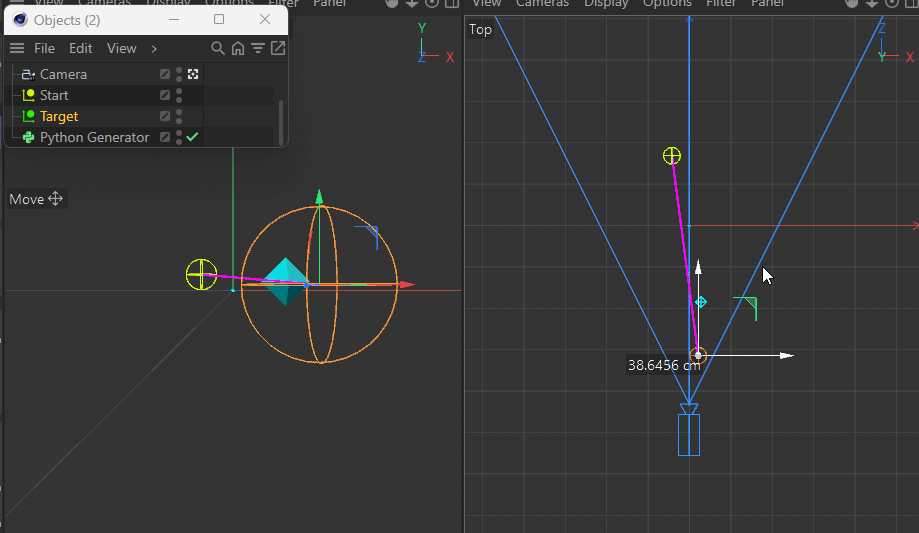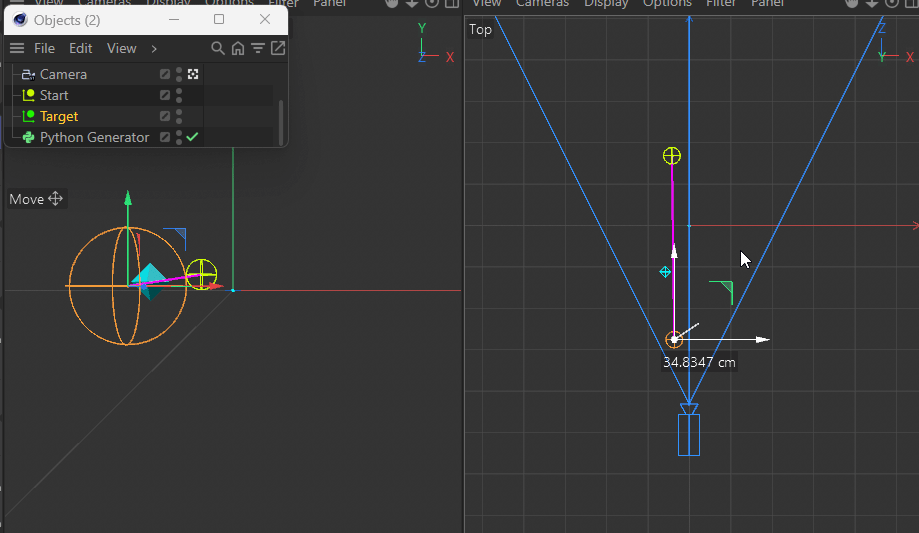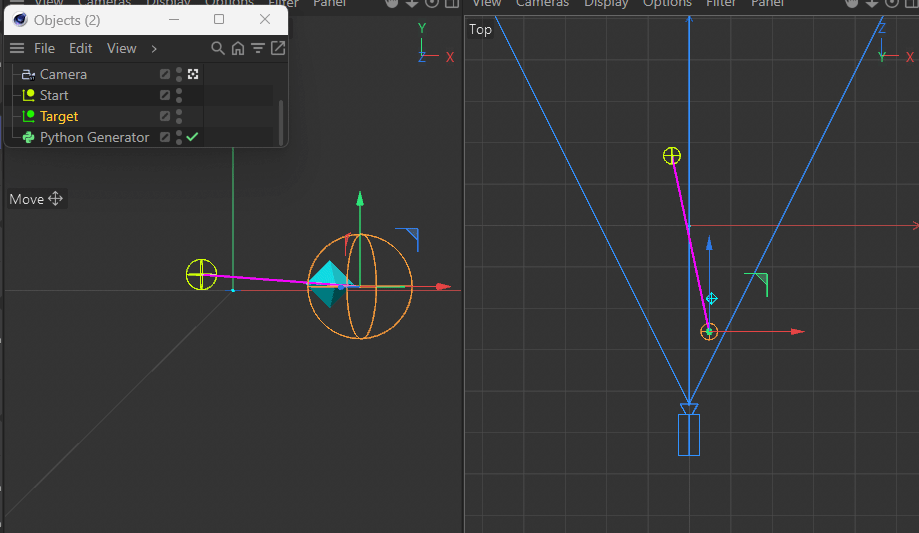
This gets more apparent when moving the target closer to the camera.Using a parallel camera (instead of perspective) of course does not have this issue.
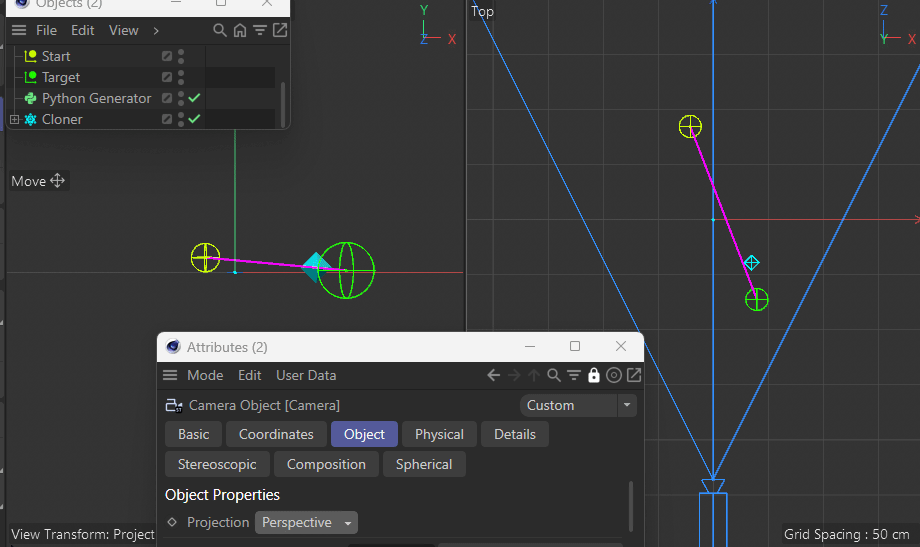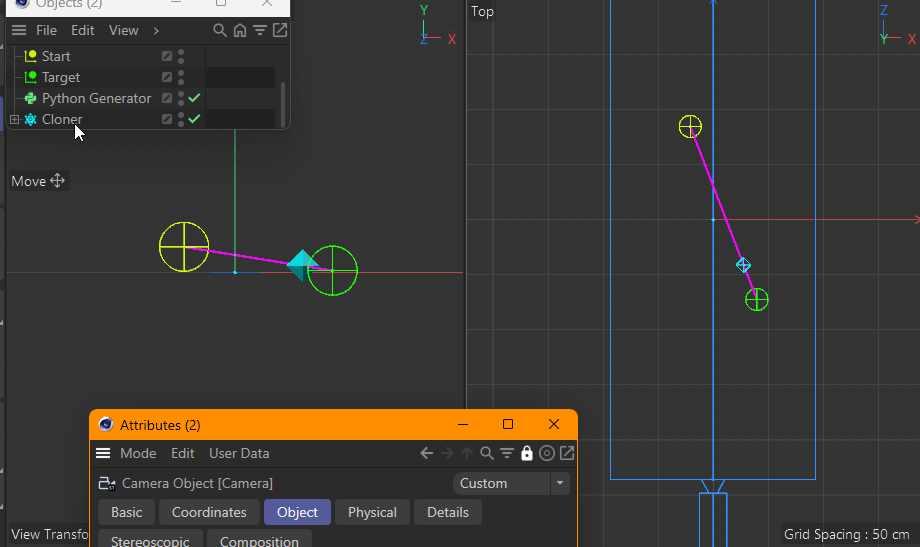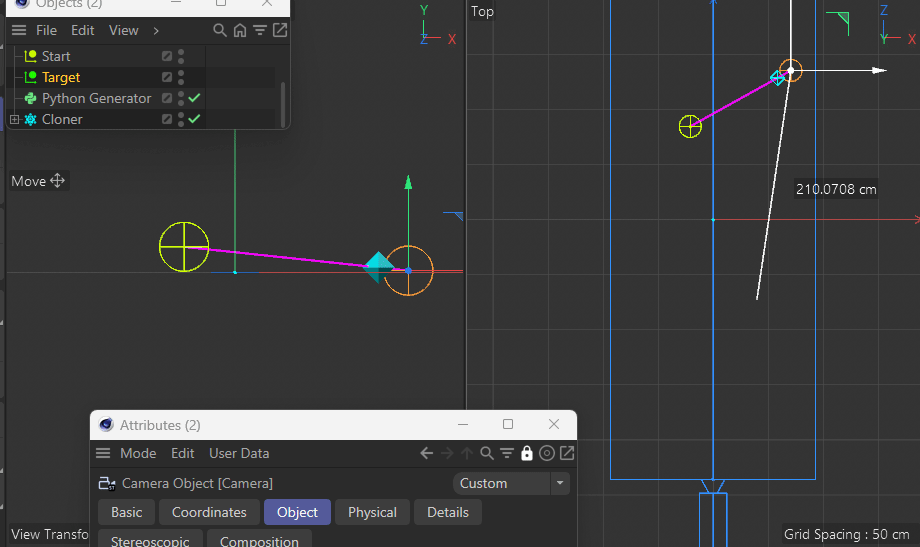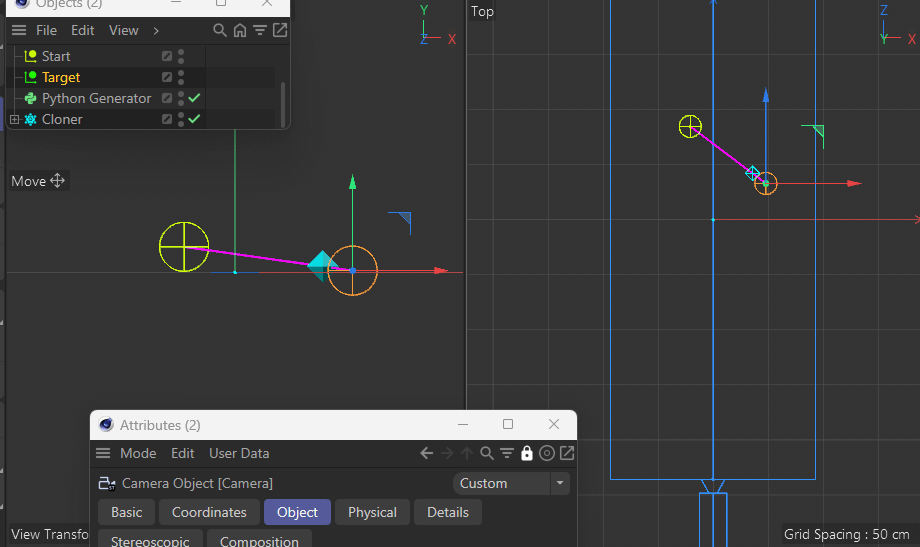
See how it's always nicely on the pink line?And that's where I'm stuck. How do I fix this? Can anyone give me a hint?
Here's my code and a demo scene.
import c4d import math doc: c4d.documents.BaseDocument # The document the object `op` is contained in. op: c4d.BaseObject # The Python generator object holding this code. hh: "PyCapsule" # A HierarchyHelp object, only defined when main is executed. def main() -> c4d.BaseObject: bd = doc.GetRenderBaseDraw() if bd is None: return c4d.BaseObject(c4d.Onull) # Note for variable names postix: # > _w = World # > _s = Screen # > _s_flat = Screen without z coordinate # World positions of start and target. start_pos_w = doc.SearchObject('Start').GetAbsPos() target_pos_w = doc.SearchObject('Target').GetAbsPos() # The distance in pixels the new point should be away from point 2. distance_from_target = 30.0 # Calculate the screen coordinates of the points. start_pos_s = bd.WS(start_pos_w) target_pos_s = bd.WS(target_pos_w) # Calling WS creates a z coordinate to describe the distance of the # point to the camera. To correctly calculate the 2D distance the # z axis must be ignored. start_pos_s_flat = c4d.Vector(start_pos_s.x, start_pos_s.y, 0) target_pos_s_flat = c4d.Vector(target_pos_s.x, target_pos_s.y, 0) # Get the direction and distance of both points in flat screen space. direction_s_flat = (target_pos_s_flat - start_pos_s_flat).GetNormalized() length_s_flat = (target_pos_s_flat - start_pos_s_flat).GetLength() # Calculate the position of the new point in screen space with respect # to the z coordinate: # 1. Calculate the ratio how far away the new point is from the # target in percent. # 1.a Subtract the distance_from_target from the flat length. length_s_flat_delta = length_s_flat - distance_from_target # 1.b Divide delta by the flat length to get the ratio. ratio = length_s_flat_delta / length_s_flat # 2. Calculate the new point in "deep" screen space. # 2.a Get direction and length of the screen space positions. direction_s = (target_pos_s - start_pos_s).GetNormalized() length_s = (target_pos_s - start_pos_s).GetLength() # 2.b Use the ratio to calculate the new point in "deep" screen space. new_point_s = start_pos_s + (direction_s * length_s * ratio) # Transform the new point to world coordinates. new_point_w = bd.SW(new_point_s) # Create some output to visualize the result. points = [start_pos_w, new_point_w, target_pos_w] poly_obj = c4d.BaseObject(c4d.Opolygon) poly_obj.ResizeObject(len(points), 0) for i, point in enumerate(points): poly_obj.SetPoint(i, point) return poly_objLink to demo scene (2024.2.0) on my OneDrive:
https://1drv.ms/u/s!At78FKXjEGEomLMOaoZcJaA2TSwblg?e=8wfev1Cheers,
Daniel - Get screen coordinates of both points using
-
Hacky Solution
I stumbled across
BaseView.ProjectPointOnLine. This takes a line in 3D space and tries to project "a given mouse coordinate" onto it. Don't know why they'd specifically point out that this is for mouse coordinates when it seems to also work for any camera screen coordinates.So here's what I did:
- Calculate the screen position of the desired point
new_point_s. - Call
BaseView.ProjectPointOnLine. Use the world position ofStartandTargetfor the line andnew_point_sfor the point to project onto the line like this:
new_point_w = bd.ProjectPointOnLine(start_pos_w, target_pos_w - start_pos_w, new_point_s.x, new_point_s.y)While this technically works it does involve more computations than I'd like it to because it does include all of this overhead of projecting that screen position onto the line which I don't believe to be the best solution to this. Imagine I actually want to work with the point in screen space before translating it back to world space, I'd have to do another round-trip of
WS-ing (to actually get the correctnew_point_swith the correct z component) and finallySW-ing that back to world again. Yikes.Proper
I stumbled across this document which I think talks about what I need:
https://www.comp.nus.edu.sg/~lowkl/publications/lowk_persp_interp_techrep.pdf
And while I don't expect you to read through those two pages what is important is (12) on page 2 which I think should translate to this:new_z = 1.0 / ( (1.0 / start_pos_w.z) + length_s_flat_delta * ( (1.0 - target_pos_w.z) - (1.0 / start_pos_w.z) ) )However this does not produce the correct result. Isn't this document talking about what I need?
Cheers,
Daniel - Calculate the screen position of the desired point
-
Hi Daniel,
Thank you for the question with a detailed explanation and an example scene. Highly appreciated attitude!
Although the thread is generally out of scope of the support, since it is almost purely algorithmic, I would anyway try to comment on a couple of your assumptions I'm not sure I agree with.
The approach with using the ProjectPointOnLine() function (exactly the same way you described it under the title "Hacky Solution") is actually the one that first came to my mind when I got through your problem. I don't completely get your point about
involve more computations than I'd like it to
Are you referring to a number of computations or the amount of time it takes for them to be executed? Assuming the second option, did you actually measure the performance of both approaches? I assume, manually performing point projection in python would actually be slower than calling this function that has implementation compiled from C++. However, even if you go with C++ plugin, I'd still doubt a couple of linear algebra formulas would take too much time.
Another point is
Imagine I actually want to work with the point in screen space before translating it back to world space
Why can't you first do your computations in screen space and only then use the ProjectPointOnLine() function?
Regarding the article you addressed, if I got it right, the author does his computations already in the camera coordinate system, so before applying the formulas from there you need to transform your positions to camera system first. Plus, it's not mentioned there in the article, but he might be using the RHS, while cinema lives in LHS. More on that in Intro to Computer Graphics: Coordinate Systems and in our Matrix Manual. Intuitively speaking, I think it is just the same math but expressed with a little different flavor.
I had another eccentrical idea (which would perhaps lead you to the same formulas after all) to express the problem as the cone frustum (or truncated cone in other words) ray intersection. Your pixel-distance (30px in your example) actually define a cone frustum in camera coordinate system (or just a cylinder if you use orthogonal camera). Your start and target objects define the ray. Then you intersect them and get the point that you were looking for. However, as I said, I think there's nothing you can gain here in terms of efficiency (especially when using python), so I personally would stick to the approach that you named as "hacky"

Cheers,
Ilia -
Good morning Ilia,
Thanks for your detailed response even though this is out of support scope!
Let me explain what I meant by this:
involve more computations than I'd like it to
Using
ProjectPointOnLine()the calculations by the script are as follows:- Transform 3D points to 2D screen space using
WS(). - Calculate my desired new point in screen space.
- Transform the new point to 3D world space by projecting the new point onto the 3D line using
ProjectPointOnLine(). - Transform the new point back from 3D world space to 2D screen space using
WS(). - Do more things using these correct 2D coordinates of the new point.
The issue of this topic is addressed by step 3 but to further work properly with the point in 2D space I also need step 4. I in fact do not only need the 2D coordinates but the z component as well. I feel like there must be a mathematical formula to get the correct Z value without transforming all three vector components back and forth in steps 3 and 4. So the issue I have with the "hacky" solution is purely to reduce the amount of performed calculations to a bare minimum which to be completely honest is just a means to satisfy this itch of mine to optimize as much as possible. It's part of what makes programming fun to me.

Also it would really be interesting to grasp the mathematical concept behind this. As someone who taught himself 3D programming by reading a bunch of game dev tutorials 15 years ago this is super interesting. But enough rambling.
Regarding your question:
Why can't you first do your computations in screen space and only then use the ProjectPointOnLine() function?
In my example the script I'm currently working on takes the new point as a base and creates some more points around that which are not on the line so I can't use
ProjectPointOnLine()for those. For that the new point must have the correct coordinates already so I can derive the other new points correctly, otherwise their position in the world will be skewed as well.
The frustum concept is something I'll have to take some time to fully understand how I can utilize that. Thanks for the hint.
Have a nice weekend,
Daniel - Transform 3D points to 2D screen space using



