Example mod_curve_lightning¶
Demonstrates how to construct curves in a tool.
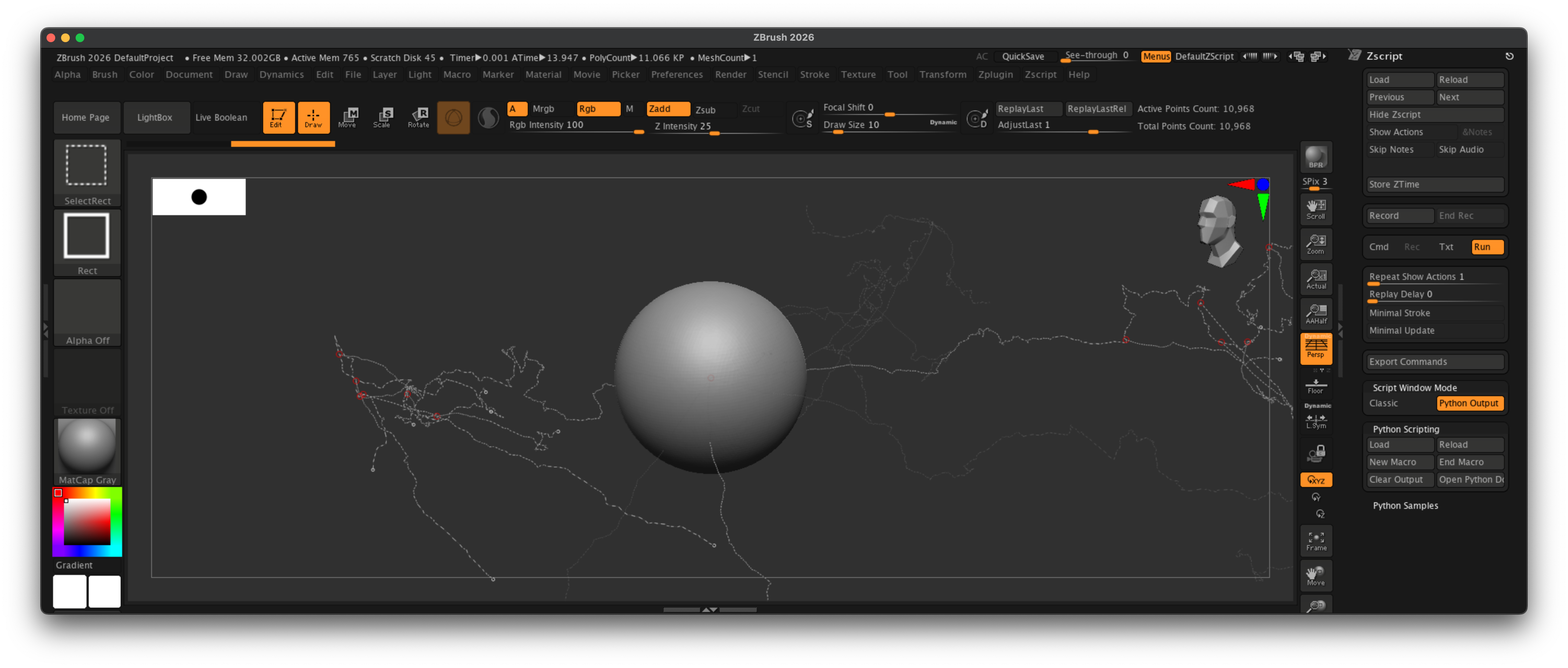
Fig. I: A possible outcome of the example.¶
Code¶
"""Demonstrates how to construct curves in a tool.
Curves are an important part of ZBrush's tool set. We can use the API to create new curves (but
we currently cannot read or modify existing curves). This example creates multiple curves deformed
by a value noise to generate output that resembles lightning arcs.
The script requires the document to have an editable PolyMesh3D tool to be activated. The script
will then select the "CurveTube" brush and create multiple lightning arcs in the active tool.
You can run this example multiple times in a row and it will generate a different effect each time.
Comment out the line `ValueNoise.SEED = random.uniform(0, 1000000)` to make the example deterministic.
Note:
By default you will only see the curve output, to see the brush applied you must move one of the
created curves a tiny bit. You can of course also switch the curve brush before applying the
curves.
"""
__author__ = "Ferdinand Hoppe"
__date__ = "22/08/2025"
__copyright__ = "Maxon Computer"
from zbrush import commands as zbc
import math
import random
import os
import sys
# --- Code for importing the local math library next to this script --------------------------------
# Extend the module search paths and import the math library next to this script.
script_dir: str = os.path.dirname(__file__)
if not script_dir in sys.path:
sys.path.insert(0, script_dir)
from lib_zb_math import Vector, ValueNoise
# It is important that we clean up after ourself, as this is shared Python instance. And our module
# might collide with the module of the same name imported by another script.
sys.path.remove(script_dir)
sys.modules.pop("lib_zb_math", None)
# --- Start of curve example -----------------------------------------------------------------------
def create_lightning(branches: tuple[int, int, int], step_size: float = 0.1,
min_length: float = 0.25, max_length: float = 2.0) -> None:
"""Generates random lightning curves.
Args:
branches: A tuple describing the number of branches of the lightning effect.
- 0: The number of main branches.
- 1: The minimum number of sub-branches per main branch.
- 2: The maximum number of sub-branches per main branch.
step_size: The resolution of the curve. This value is interpreted in the coordinate system
of the active tool, i.e., the scale of the effect scales with the tool it is
applied to.
min_length: The minimum length of a main branch.
max_length: The maximum length of a main branch.
"""
# Start a new set of curves, deleting any existing not yet applied curves.
zbc.new_curves()
# Loop over the main branches.
for _ in range(branches[0]):
# Create a new curve, chose a random length for it, and compute the number of steps, i.e.,
# points that will fit into it. Finally, compute a random direction for the curve.
cid: int = zbc.add_new_curve()
length: float = random.uniform(min_length, max_length)
steps: int = int(length / step_size)
direction: Vector = Vector(random.uniform(0, 2 * math.pi),
random.uniform(0, 2 * math.pi),
random.uniform(0, 2 * math.pi))
# Now build the points for the curve. #t is the relative offset along the curve, e.g., 0.5
# for 50% and #p is the absolute offset, e.g., 5 units at t=0.5 for a 10 units long curve.
points: list[Vector] = []
for t, q in [(i / steps, i * step_size) for i in range(steps)]:
# Compute the base point, i.e., a line point at #t. We just construct a line along the
# z-axis and then rotate it into position.
p: Vector = Vector(0, 0, q).rotate(direction)
# Now we sprinkle a bit of noise onto our point to achieve the 'lightning' effect. We
# multiply the effect by #t so that it is null at the tip of the curve and the strongest
# at its end. We add #cid to the relative offset #q so that each curve is unique.
p += ValueNoise.turbulence_13(cid + q, 2.0, 8) * t
# And finally we add the point to the curve and our list of points (so that we can later
# pick points for the sub-branches).
zbc.add_curve_point(cid, p.x, p.y, p.z)
points.append((t, p))
# Now we are going to create the sub-branches. This could of course be done recursively to
# generate high fidelity lightning effects but we keep it simple here. We pick a random
# number of sub-branches and then iterate over them.
for _ in range(random.randint(branches[1], branches[2])):
# Now we are going to pick a relative offset #t along the main branch where the sub-
# branch should start. We compute a random offset and raise it by 1/2 to make it more
# likely that we pick a value at the end of the curve. Then we search for the point
# #mPoint in our points whose relative offset #mt is larger than or equal to #t.
t: float = random.uniform(0, 1) ** 0.5
mt, mPoint = next(((mt, mPoint) for mt, mPoint in points if mt >= t), (0, 0))
# And now it is basically just the same over again.The only thing that is slightly
# different is that we use the relative offset #mt along the main branch to scale the
# sub-branch and that the sub-branch starts at #mPoint instead of (0, 0, 0).
sub_cid: int = zbc.add_new_curve()
sub_length: float = random.uniform(min_length * mt * 0.3, max_length * mt * 0.3)
sub_steps: int = int(sub_length / step_size)
sub_direction: Vector = Vector(random.uniform(0, 2 * math.pi),
random.uniform(0, 2 * math.pi),
random.uniform(0, 2 * math.pi))
for st, sp in [(i / sub_steps, i * step_size) for i in range(sub_steps)]:
p: Vector = mPoint + Vector(0, 0, sp).rotate(sub_direction)
p += ValueNoise.turbulence_13(sub_cid + sp, 2.0, 8) * st * mt
zbc.add_curve_point(sub_cid, p.x, p.y, p.z)
# Copy all the curves we created to the UI.
zbc.curves_to_ui()
def main() -> None:
"""Executed when cell_zBrush runs this script.
"""
# Make sure that the active tool is editable and enable the CurveTube brush.
if not zbc.is_enabled("Transform:Edit"):
return zbc.show_note("Active tool is not editable.", display_duration=2.0)
if not zbc.exists("Brush:CurveTube"):
return zbc.show_note("No 'CurveTube' brush found.", display_duration=2.0)
zbc.set("Transform:Edit", True)
zbc.press("Brush:CurveTube")
zbc.set("Draw:Draw Size", 10)
# Randomize the value noise seed and then create lightning effect. Be careful with Python's
# random.seed function, it is extremely expensive to call. One call is absolutely fine but
# you should not write scripts which call this function hundreds or thousands of times. Use
# then something like #ValueNoise.hash_31 instead.
ValueNoise.SEED = random.uniform(0, 1000000)
random.seed(ValueNoise.SEED) # Ensure reproducibility for the example.
create_lightning(branches=(3, 4, 8), # number of main branches and min max sub-branch count.
step_size=0.01, # The resolution of the curve.
min_length=6.0, # The minimum length of a main branch.
max_length=10.0) # The maximum length of a main branch.
if __name__ == "__main__":
main()