Hello coders,
since this is a question about algorithms I figured I'd post this here. Also this is mostly me hoping that someone will drop some wisdom on me in terms of 3D programming.
Problem
So I got two different positions in 3D space, Start and Target. When I look at them in the C4D viewport I need to calculate a new point which is between the two points, but 30 pixels before the target.
Take a look at this example where the distance in pixels on the screen is 298, so I need a new point which is 268 pixels away from Start (298px - 30px), blue X marks the desired spot.
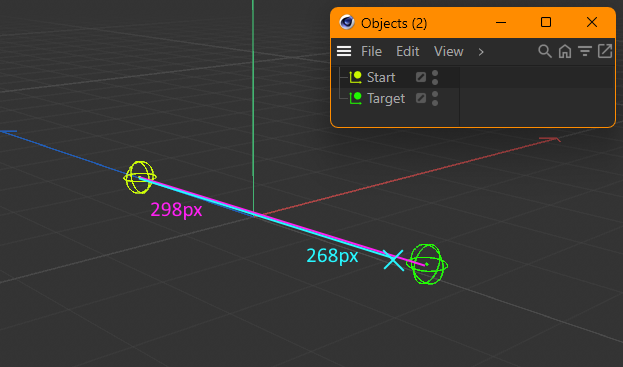
However this point must exist in world space.
So my thought process was this:
- Get screen coordinates of both points using
BaseView.WS.
- Calculate how far away the new point is from
Start in percent relative to the screen distance to Target.
- Create a new point in screen space using this calculated ratio by doing
Start + Direction * Distance * Ratio.
- Transform to world coordinates using
BaseView.SW.
The new point will be in the correct screen coordinates, so x and y are fine. However z is messed up which I can only assume is because of the camera perspective.
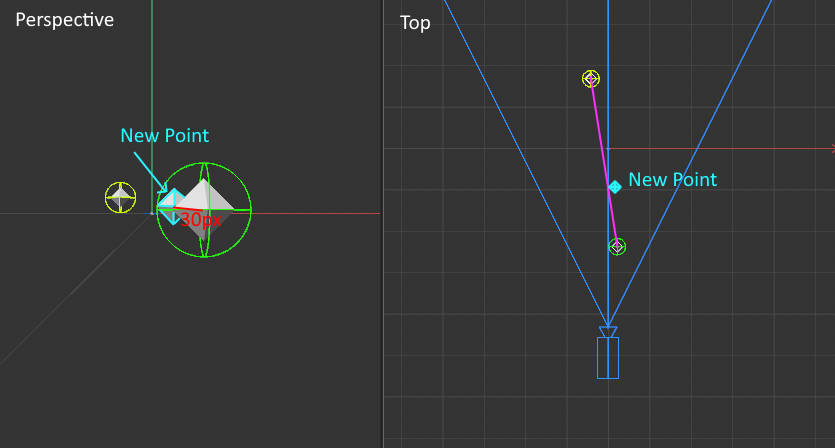
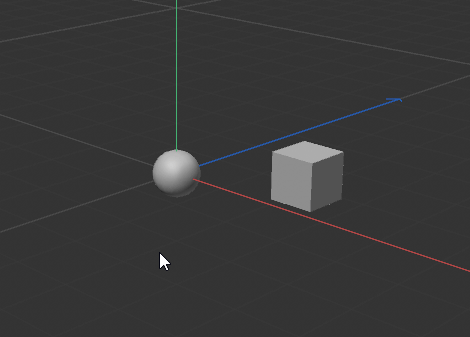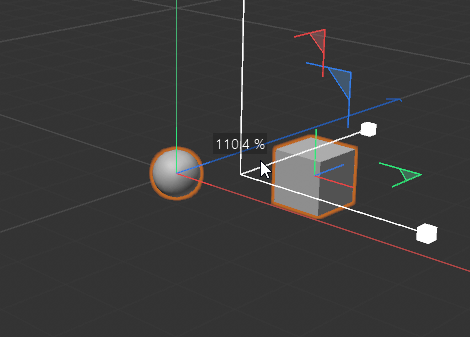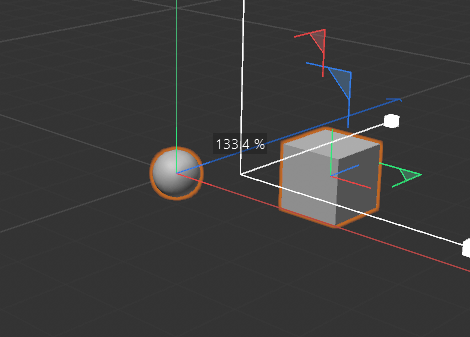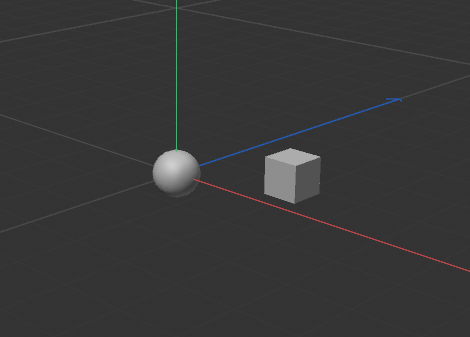
Note in the following demo how both the target and the new point are always the same distance apart from each other in Perspective View while the z coordinate in Top View prevents the point from being on the desired pink line between the two points:
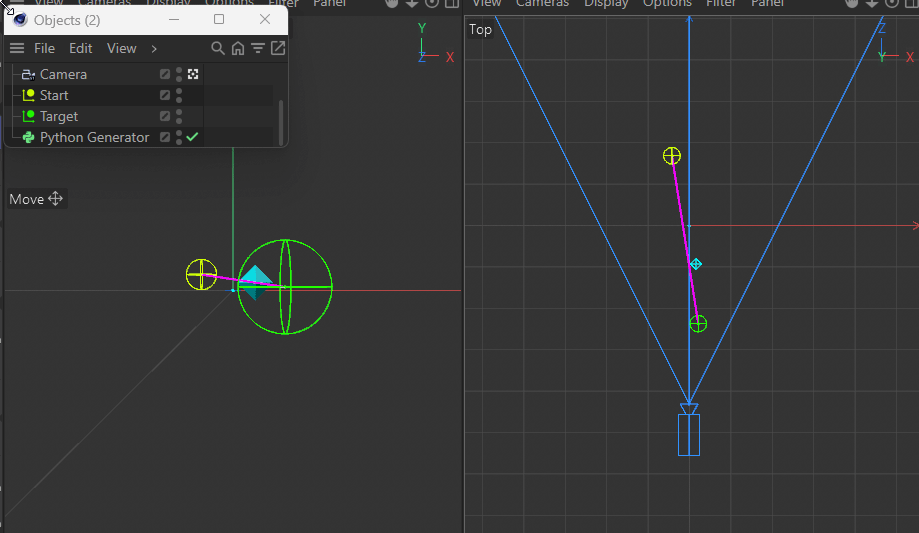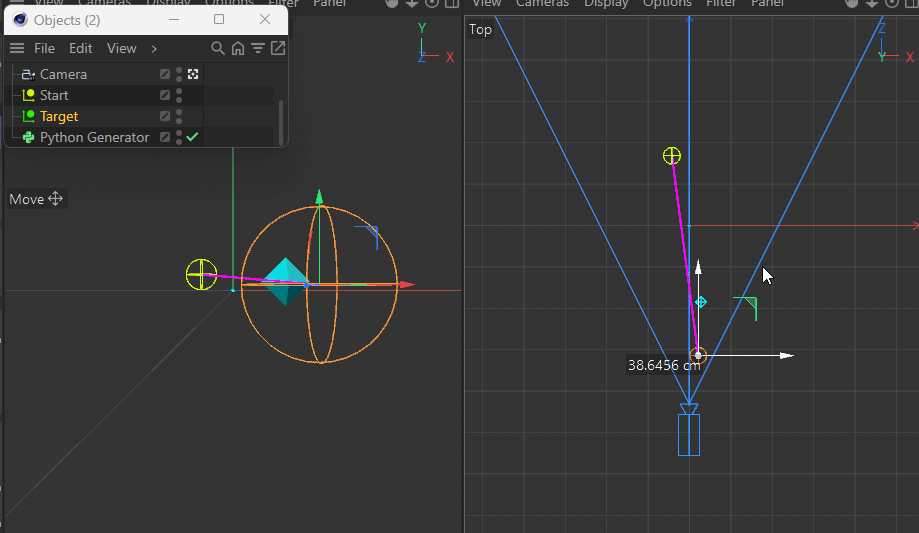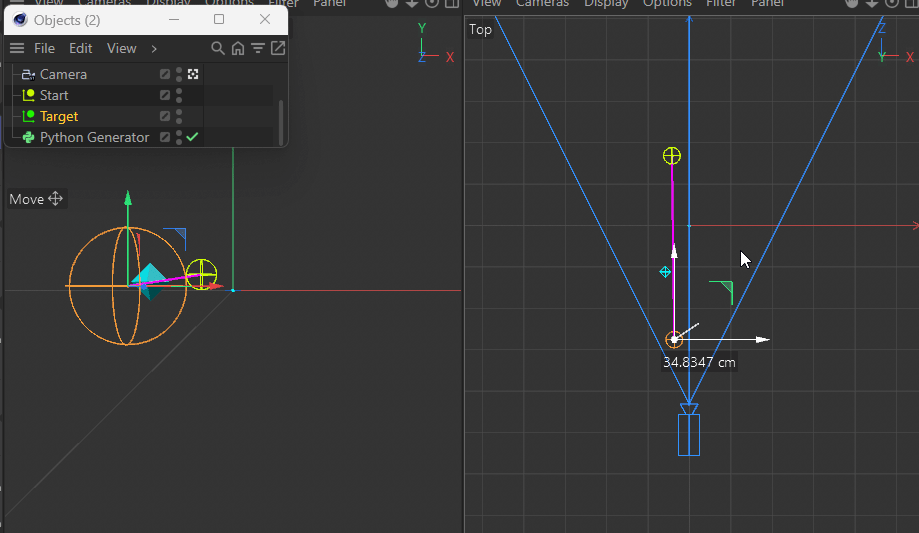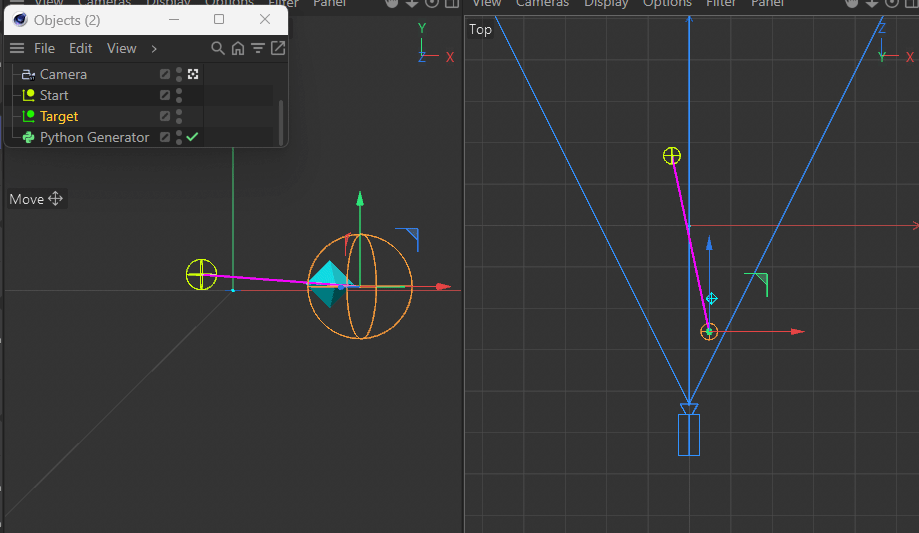
This gets more apparent when moving the target closer to the camera.
Using a parallel camera (instead of perspective) of course does not have this issue.
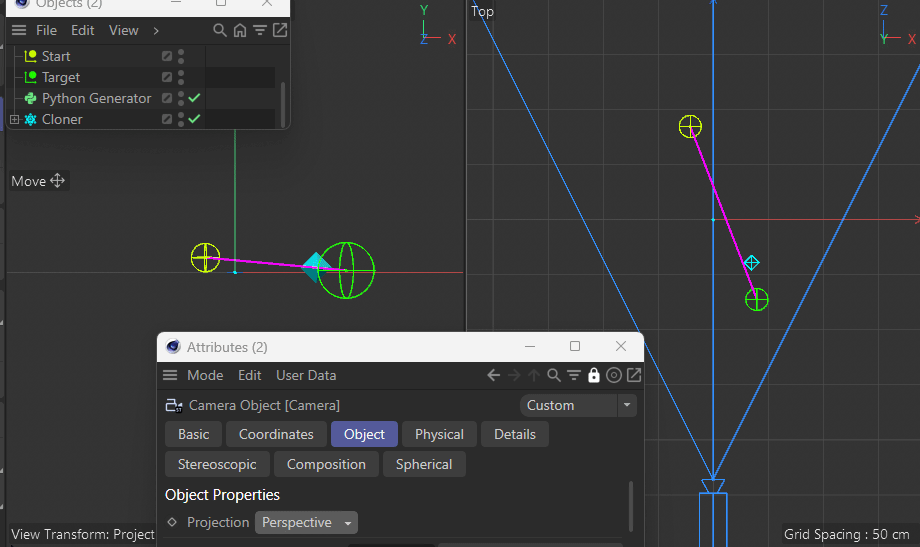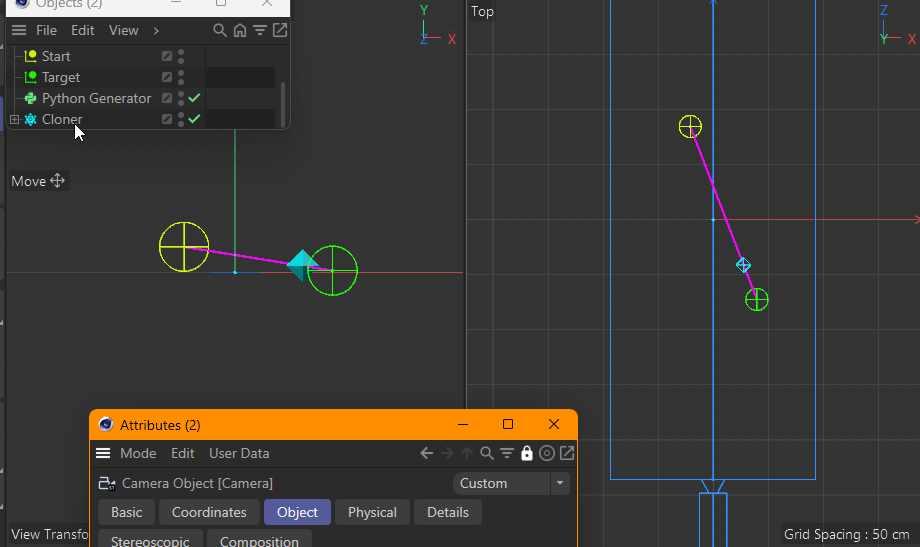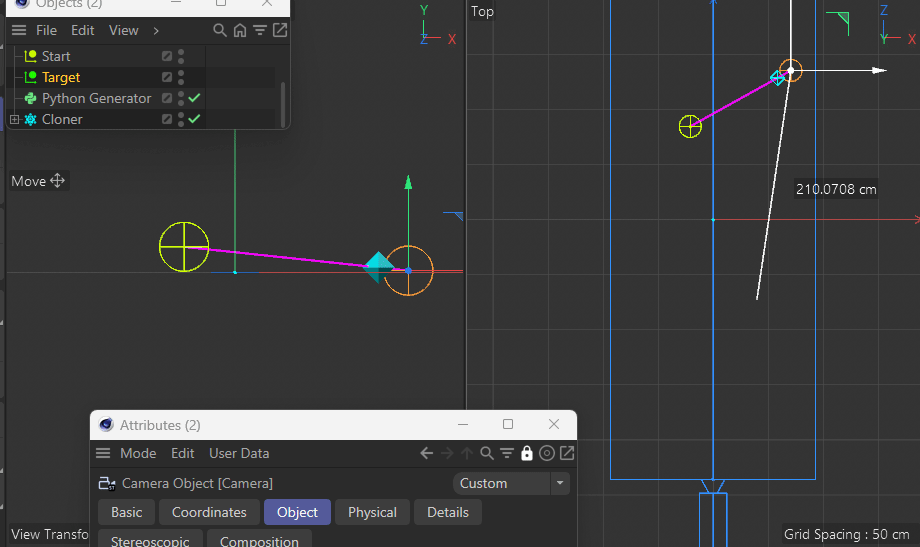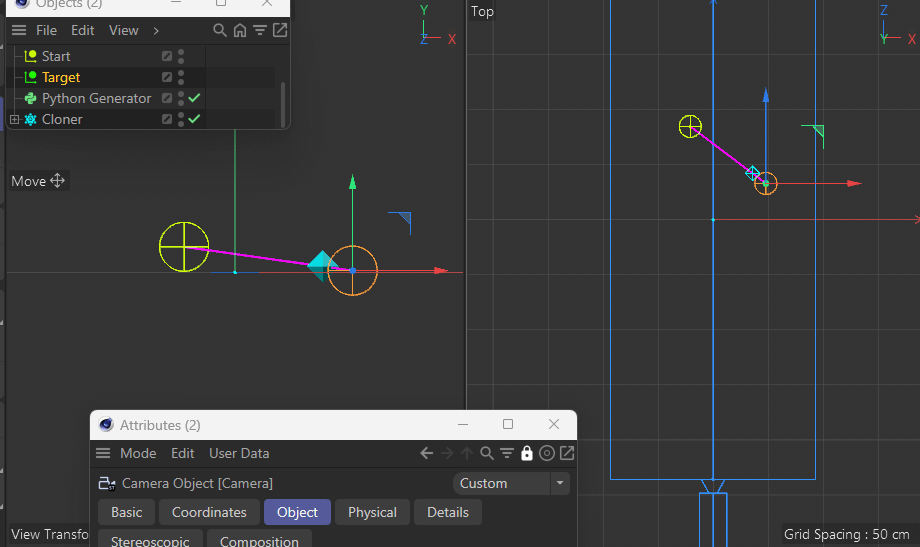
See how it's always nicely on the pink line?
And that's where I'm stuck. How do I fix this? Can anyone give me a hint?
Here's my code and a demo scene.
import c4d
import math
doc: c4d.documents.BaseDocument # The document the object `op` is contained in.
op: c4d.BaseObject # The Python generator object holding this code.
hh: "PyCapsule" # A HierarchyHelp object, only defined when main is executed.
def main() -> c4d.BaseObject:
bd = doc.GetRenderBaseDraw()
if bd is None:
return c4d.BaseObject(c4d.Onull)
# Note for variable names postix:
# > _w = World
# > _s = Screen
# > _s_flat = Screen without z coordinate
# World positions of start and target.
start_pos_w = doc.SearchObject('Start').GetAbsPos()
target_pos_w = doc.SearchObject('Target').GetAbsPos()
# The distance in pixels the new point should be away from point 2.
distance_from_target = 30.0
# Calculate the screen coordinates of the points.
start_pos_s = bd.WS(start_pos_w)
target_pos_s = bd.WS(target_pos_w)
# Calling WS creates a z coordinate to describe the distance of the
# point to the camera. To correctly calculate the 2D distance the
# z axis must be ignored.
start_pos_s_flat = c4d.Vector(start_pos_s.x, start_pos_s.y, 0)
target_pos_s_flat = c4d.Vector(target_pos_s.x, target_pos_s.y, 0)
# Get the direction and distance of both points in flat screen space.
direction_s_flat = (target_pos_s_flat - start_pos_s_flat).GetNormalized()
length_s_flat = (target_pos_s_flat - start_pos_s_flat).GetLength()
# Calculate the position of the new point in screen space with respect
# to the z coordinate:
# 1. Calculate the ratio how far away the new point is from the
# target in percent.
# 1.a Subtract the distance_from_target from the flat length.
length_s_flat_delta = length_s_flat - distance_from_target
# 1.b Divide delta by the flat length to get the ratio.
ratio = length_s_flat_delta / length_s_flat
# 2. Calculate the new point in "deep" screen space.
# 2.a Get direction and length of the screen space positions.
direction_s = (target_pos_s - start_pos_s).GetNormalized()
length_s = (target_pos_s - start_pos_s).GetLength()
# 2.b Use the ratio to calculate the new point in "deep" screen space.
new_point_s = start_pos_s + (direction_s * length_s * ratio)
# Transform the new point to world coordinates.
new_point_w = bd.SW(new_point_s)
# Create some output to visualize the result.
points = [start_pos_w, new_point_w, target_pos_w]
poly_obj = c4d.BaseObject(c4d.Opolygon)
poly_obj.ResizeObject(len(points), 0)
for i, point in enumerate(points):
poly_obj.SetPoint(i, point)
return poly_obj
Link to demo scene (2024.2.0) on my OneDrive:
https://1drv.ms/u/s!At78FKXjEGEomLMOaoZcJaA2TSwblg?e=8wfev1
Cheers,
Daniel